調和数は整数にならない ~ 一般化と証明
2023年3月16日
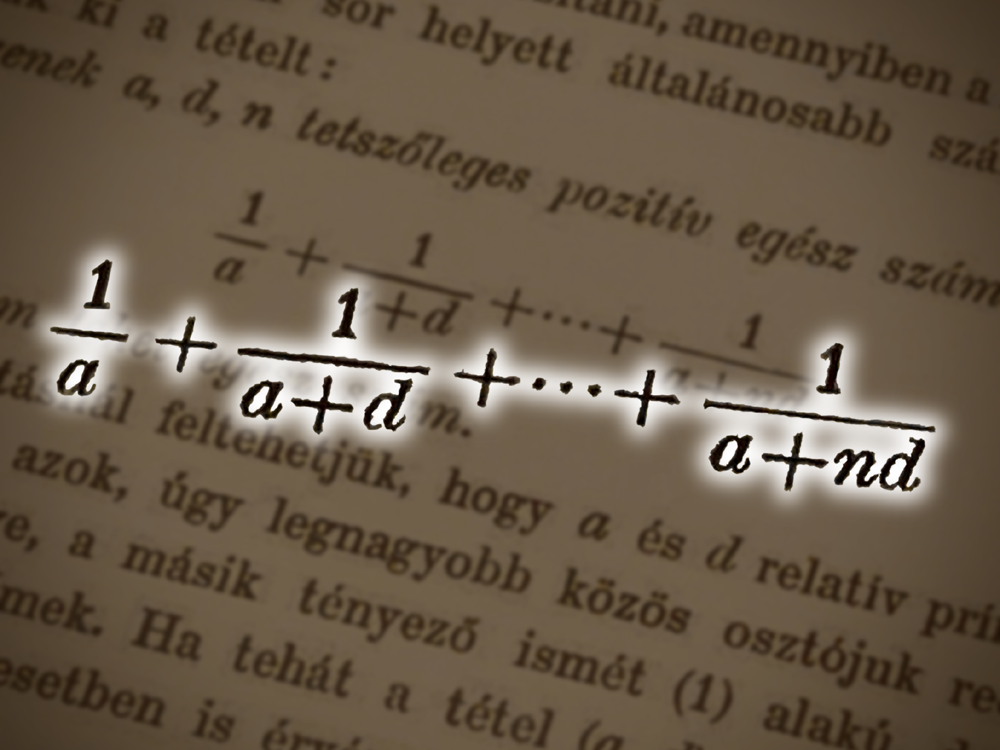
自然数 $n$ に対し,第 $n$ 調和数(harmonic number)$H_n$ を
$n\geqq 2$のとき,$H_n$の値は整数にならないことが知られています.
これは割と有名な結果で,高校生向けの受験参考書にも証明問題が掲載されているのを見たことがあります($n$ が素数の場合が出題されていたと記憶しています).
この結果にはいろいろな拡張が知られていますが,それらの一部をまとめると次のようになります:
きれいに段階的な拡張になっていますね!
この記事では,定理3の証明を最終目標に,途中で定理2の証明もご紹介します.
\[ H_n=1+\dfrac{1}{2}+\dfrac{1}{3}+\cdots+\dfrac{1}{n} \]
と定義します.$n\geqq 2$のとき,$H_n$の値は整数にならないことが知られています.
これは割と有名な結果で,高校生向けの受験参考書にも証明問題が掲載されているのを見たことがあります($n$ が素数の場合が出題されていたと記憶しています).
この結果にはいろいろな拡張が知られていますが,それらの一部をまとめると次のようになります:
定理1(タイシンガー,1915年)
$n$ を $2$ 以上の整数とするとき,
\[ 1+\dfrac12+\dfrac13+\dots+\dfrac1n \]
は整数にならない.
定理2(クルシャーク,1918年)
$a$,$n$ を正の整数とするとき,
\[ \dfrac{1}{a}+\dfrac{1}{a+1}+\dots+\dfrac{1}{a+n} \]
は整数にならない.
定理3(エルデシュ,1932年)
$a$,$d$,$n$ を正の整数とするとき,
\[ \dfrac{1}{a}+\dfrac{1}{a+d}+\cdots+\dfrac{1}{a+nd} \]
は整数にならない.
この記事では,定理3の証明を最終目標に,途中で定理2の証明もご紹介します.
この記事を書くきっかけになったのは,Twitterで,定理3の $a=1$,$d=6$ の場合の証明が数学検定1級の2次試験で出題されたというツイートを見たからです(数検の過去問をピンポイントで見つけるのは難しく,私自身はその問題を確認出来ておりません^^;).
定理3の結果だけは知っていたのですが,証明したことはなかったので,この度証明を追ってみることにしました!
追っていくうちに,「これはTwitterでは余白が狭すぎる」と感じたので(笑)ブログの記事にすることにしました.
証明に入る前に記号を定めておきます.
正の整数 $a$,$d$,$n$ に対し,
また,$a$ と $d$ が互いに素でないとき,$g=\gcd(a,\,d)$ とすると,$a=ga^\prime$,$d=gd^\prime$,$\gcd(a^\prime,\,d^\prime)=1$ と表わされるので,
よって以下の証明において,$\boldsymbol{a}$ と $\boldsymbol{d}$ は互いに素であると仮定します.
また,$a\gt n$ とすると,
よって,$\boldsymbol{a\leqq n}$ も仮定します.
なので,$d=1,\,2,\,3$ の場合は個別に証明する必要があります.
本節では $d=1$ の場合,すなわち定理2を証明しようと思います.
実は,$d=1$ の場合の証明は,あとで述べる $d$ が正の奇数の場合の証明に含まれているのですが,他の場合の証明に慣れるという意味も込めて,$d=1$ の場合の証明は個別に述べようと思います.
証明すべきことは,
他の場合の証明にも共通することですが,$a$,$a+1$,$\cdots$,$a+n$ の中で特別な素数の累乗を約数にもつ項の存在を示し,それを利用して証明していきます.
$d=1$ の場合は,素数 $2$ に注目します!
$a$,$a+1$,$\cdots$,$a+n$ の中に $2$ で割り切れる項が存在しますが,その中で最も多くの回数 $2$ で割り切れるもので最小の項を $a+k\,\,(0\leqq k\leqq n)$ とします.
次に,$2$ で $\alpha$ 回割り切れるものは $a+k$ 以外にないことを示します.
$a+k$ 以外に $2^\alpha$ で割り切れる項があるとして,それを
$a+k\lt a+l$ より,$x\lt y$ であり,$x$,$y$ はともに奇数なので,
以上により,$a$,$a+1$,$\cdots$,$a+n$ の中で $2^\alpha$ で割り切れるものは $a+k$ だた1つであることが分かりました.
次に,$a$,$a+1$,$\cdots$,$a+n$ の最小公倍数を $L$ とします.$L$ は $2$ でちょうど $\alpha$ 回割り切れます.
一方右辺において,項はすべて整数であり,$\dfrac{L}{a+k}$ 以外の項については,分子 $L$ は $2$ で $\alpha$ 回割り切れ,分母は $2$ で $\alpha-1$ 回以下しか割り切れないのですべて偶数になります.
$\dfrac{L}{a+k}$ のみ,分子・分母がともに $2$ でちょうど $\alpha$ 回割り切れるので奇数になります.
偶数の和に1つだけ奇数を加えたものなので右辺は奇数になりますが,左辺は偶数だったのでこれは矛盾です!!
以上により,$S(a,\,1,\,n)$ は整数にならないことが示されました.
$a$ と $d$ が互いに素である場合を考えればよいので,$a$ は奇数です.
分母には,$a$ から $a+2n$ までのすべての奇数が現れます.
$a\leqq n$ より,
$a$,$a+2$,$\cdots$,$a+2n$ の中に $3$ の倍数が存在することが分かったので,その中で最も多くの回数 $3$ で割り切れるもので最小の項を $a+2k\,\,(0\lt k\leqq n)$ とします.
次に,$x=1$ であることを示します.
まず,$a\leqq 3^\alpha$ を示します.もし $3^\alpha\lt a$ であるとすると,$3^{\beta}\lt a$ をみたす最大の正整数 $\beta$ をとるとき,
また,$a+2n\lt 3^\alpha$ とすると,$a$,$a+2$,$\cdots$,$a+2n$ の中に $3^\alpha$ で割り切れるものが存在しなくなり $\alpha$ の選び方に反するので,$3^\alpha \leqq a+2n$ です.
よって,$a$,$a+2$,$\cdots$,$a+2n$ の中に $3^\alpha$ と一致するものが存在し,$k$ の選び方から,
$a$,$a+2$,$\cdots$,$a+2n$ の中に $3^\alpha$ で割り切れる項がもう1つあると仮定して,その項を
よって,$a$,$a+2$,$\cdots$,$a+2n$ の中で $3$ で $\alpha$ 回割り切れるものは $a+2k$ のみであり,他の項は $3$ で $\alpha-1$ 回以下しか割り切れないことが分かりました.
$a$,$a+2$,$\cdots$,$a+2n$ の最小公倍数を $L$ とします.$L$ は $3$ でちょうど $\alpha$ 回割り切れます.
$S(a,\,2,\,n)$ が整数であると仮定して,
一方右辺において,項はすべて整数であり,$\dfrac{L}{a+2k}$ 以外の項については,分子 $L$ は $3$ で $\alpha$ 回割り切れ,分母は $3$ で $\alpha-1$ 回以下しか割り切れないのですべて $3$ の倍数になります.
$\dfrac{L}{a+2k}$ のみ,分子・分母がともに $3$ でちょうど $\alpha$ 回割り切れるので $3$ の倍数になりません.
よって右辺は $3$ の倍数になりませんが,左辺は $3$ の倍数だったのでこれは矛盾です!!
以上により,$S(a,\,2,\,n)$ は整数にならないことが示されました.
本節では $d=3$ の場合の証明にかえて,$d$ が正の奇数の場合の証明をご紹介します.以下,$d$ は正の奇数であるとします.
証明すべきことは,
$a$,$a+d$,$\cdots$,$a+nd$ の中に $2$ で割り切れる項が存在しますが,その中で最も多くの回数 $2$ で割り切れるもので最小の項を $a+kd\,\,(0\leqq k\leqq n)$ とします.
次に,$a+kd$ 以外に $2^\alpha$ で割り切れる項が複数あるとして,それらの中で2番目に小さい項を,
以上により,$a$,$a+d$,$\cdots$,$a+nd$ の中で $2^\alpha$ で割り切れるものは $a+kd$ だた1つであることが分かりました.
次に,$a$,$a+d$,$\cdots$,$a+nd$ の最小公倍数を $L$ とします.$L$ は $2$ でちょうど $\alpha$ 回割り切れます.
一方右辺において,項はすべて整数であり,$\dfrac{L}{a+kd}$ 以外の項については,分子 $L$ は $2$ で $\alpha$ 回割り切れ,分母は $2$ で $\alpha-1$ 回以下しか割り切れないのですべて偶数になります.
$\dfrac{L}{a+kd}$ のみ,分子・分母がともに $2$ でちょうど $\alpha$ 回割り切れるので奇数になります.
すなわち,左辺は偶数,右辺は奇数となり矛盾を得ました!
以上により,$d$ が正の奇数のとき,$S(a,\,d,\,n)$ は整数にならないことが示されました.
いよいよメインの $d\geqq 4$ の場合の証明に入りましょう!
本節では,証明に必要な補題の1つを証明します.
補題の主張を述べるために,記号を用意します.
正の整数 $n$ と $0\leqq k\leqq n$ をみたす整数 $k$ に対し,二項係数 $\dbinom{n}{k}$ を
次に,実数 $x$ に対し,$x\geqq n$ をみたす最大の整数 $n$ を $\lfloor x\rfloor$ で表します.例えば,$\lfloor 2\rfloor=2$,$\lfloor \pi\rfloor=3$ です.これも高校数学では,ガウス記号 $[x]$ で表わすのが主流ですね!
また,実数 $x$ に対し,$x\leqq n$ をみたす最小の整数 $n$ を $\lceil x\rceil$ で表します.例えば,$\lceil 2\rceil=2$,$\lceil \pi\rceil=4$ です.
以上で記号の準備が整ったので,補題1の主張を述べましょう:
数列 $a_1$,$a_2$,$\cdots$,$a_m$ を,
…次々と新しい記号が登場して混乱しそうですね^^;
証明は数学的帰納法で行いますが,$n\leqq 10$ の場合は個別に示す必要があります.
補題1の「感じ」をつかむために,$n=10$ の場合を計算してみます.
$n=10$ のとき,$2^3\lt 10\leqq 2^4$ より $m=4$ で,
$n\leqq 9$ の場合も同様にして示せます:
帰納法による証明に入る前に,1つ補題を準備します:
数学的帰納法で示します.
$n=5$ のとき,
ある $n\geqq 5$ での成立を仮定すると,
数学的帰納法により,補題Aが示されました.
準備が整ったので証明に入りましょう!
$n\leqq 10$ の場合は既に示したので,$n\geqq 11$ とし,$n$ より小さい正の整数に対しては補題1が成り立っていると仮定します(このとき,$m\geqq 4$ です).
我々の目標は,
ここで,$2a_2-1$に注目します.$a_2=\bigg\lceil\dfrac{n}{2^2}\bigg\rceil$より,$\dfrac{n}{2^2}\leqq a_2\lt\dfrac{n}{2^2}+1$ なので,
すなわち,$l$ を $2a_2-1\leqq 2^l$ をみたす最小の整数とし,
$a_1$,$a_2$,$\cdots$,$a_m$ と $b_1$,$b_2$,$\cdots$,$b_l$ の間の関係を調べましょう.
$2^{m-1}\lt n\leqq 2^m$ より,$2^{m-3}+1\leqq a_2=\bigg\lceil\dfrac{n}{4}\bigg\rceil\leqq 2^{m-2}$ なので,
また,
$2\leqq k\leqq l$ に対しても,$b_k=a_{k+1}$ が成り立つことを示します.
そのために,$n=2^{k+1}q+r\,\,(0\leqq r\lt 2^{k+1})$ と表わして,$a_{k+1}$ と $b_k$ を計算します.
$r=0$ のとき,
$0\lt r\lt 2^{k+1}$ のとき,
以上により,
また,$n\geqq 11$ より,$a_1=\bigg\lceil\dfrac{n}{2}\bigg\rceil\geqq 6$ なので,補題Aを $a_1$ に適用することができ,
よって,
その前に,また新たな記号を導入します.
積の記号 $\prod$ の左上にアスタリスクをつけた記号 $\sideset{^\ast}{}{\prod}$ で,素数のみの積をとる記号を表わすことにします.
ただし,条件に合う素数がないときは値が $1$ であると決めておきます.
例えば,
この記号を用いて,補題2は次のように述べられます:
このとき,
かなり難解な公式ですね^^;
補題2の「感じ」をつかむために,$n=30$ の場合を計算してみましょう(あまり小さな数だと「感じ」がつかみにくいので^^;).
$n=30$ のとき,$2^4\lt 30\leqq 2^5$ より $m=5$ で,
左辺の積を1つ1つ見ると,
ですが,このような単純に両辺の素数の個数を比較するような方法は,一般の $n$ の場合には適用できそうもありません.
そこで,区間を上手に分割して素数の数を比べるという方法をとります.
補題2の仮定のもとで,$\alpha$,$k$ を $1\leqq \alpha,\, k\leqq m$ をみたす整数とし,区間
このように定義した区間は,次の性質をもちます:
② $1\leqq k\leqq m$ のとき,区間
まず,
$1\leqq k\leqq m-1$ とします.
次に,$1\leqq k\leqq m$ を1つ固定して,$1\leqq \alpha\leqq m-1$ に対し,
もし,$1\leqq a_k\lt 2^\alpha$ だとすると,$\sqrt[\alpha+1]{2a_k}\lt 2$ なので,
$a_k\geqq 2^\alpha$ だとすると,この不等式の両辺に $a_k{}^\alpha$ をかけて,
以上で,補題Bの証明終了です!
補題Bに続けて,次の補題Cも示します:
証明には,初等整数論では良く知られている,次の定理を利用します:
このとき,$n!$ が $p$ で割り切れる回数は,
この定理を利用して,二項係数 $\dbinom{2n}{n}$ の分子・分母における素因数 $p$ の個数を比べていきます.
いま,$\lfloor\sqrt[\alpha]{n}\rfloor\lt p\leqq\lfloor\sqrt[\alpha]{2n}\rfloor$ であり,$p$ が整数であることから,$\sqrt[\alpha]{n}\lt p\leqq\sqrt[\alpha]{2n}$ なので,
よって,$(2n)!$ が $p$ で割り切れる回数は,
よって,二項係数 $\dbinom{2n}{n}$ は $p$ で割り切れることが示されました.
以上の2つの補題を用いて,補題2の不等式
証明の方針としては,左辺の素因数が,常に右辺の素因数にもなっていることを示します.
左辺の素因数の1つを $p$ とします.$p$ はどこかの積のグループに含まれているので,その1つを
補題B①より,
$p$ を含む区間の1つを,$\lfloor\sqrt[\alpha]{a_k}\rfloor\lt x\leqq\lfloor\sqrt[\alpha]{2a_k}\rfloor$ とすると,補題Cにより,$\dbinom{2a_k}{a_k}$ は $p$ を素因数にもちます.
不等式 $(\ast)$ の左辺が素因数 $p$ を複数個もっている場合を考えます.
素因数 $p$ を2つもっている場合,その2つは異なる積のグループからとり出されているので,それらを,
もし,$a_k=a_l$であるとすると,区間
よって,$a_k\neq a_l$ であり,$\dbinom{2a_k}{a_k}$,$\dbinom{2a_l}{a_l}$ がともに $p$ を素因数にもちます.
このように,$(\ast)$ の左辺が $p$ で割り切れる回数に応じて,右辺で $p$ で割り切れる二項係数を選び出すことができます.
これは,不等式 $(\ast)$ が成り立つことを示しており,補題2が証明されました!
本節では,$d\geqq 4$ の場合の証明のための最後の補題を準備します:
このとき,素数 $p$ と正の整数 $\alpha$ で,$p^\alpha\gt n$ かつ,
背理法で証明するために,
矛盾を導くために,
ここで,$p$ を素数として,$(\ast\ast)$ の中に $p$ で割り切れる項 $a+kd$ が存在するとします.このとき,$d$ は $p$ で割り切れません.もし $d$ が $p$ で割り切れるとすると,$a$ も $p$ で割り切れることになり,$a$ と $d$ が互いに素であるという条件に反するからです.
素数 $p$ が $p\gt n$ をみたすとき,仮定により $(\ast\ast)$ の中に $p$ で割り切れる項はありません.もちろん $n!$ も割り切れません.
素数 $p$ が $\sqrt{n}\lt p\leqq n$ をみたすとき,$\dfrac{n}{p^2}\lt 1\leqq\dfrac{n}{p}$ とルジャンドルの定理より,$n!$ は $p$ でちょうど $\bigg\lfloor\dfrac{n}{p}\bigg\rfloor$ 回割り切れます.
$(\ast\ast)$ の中で,$p$ で割り切れるものが存在するとして,その中で最小のものを $a+k_1d=px$,2番目に小さいものを $a+k_2d=py$ とします.差をとると,
以上の考察から,$(\ast\ast)$ の中で $p$ で割り切れるものは,
$p^2\gt n$ より,$(\ast\ast)$ に $p^2$ で割り切れる項はないので,$P(a,\,d,\,n)$ の分子は,$p$ で最大でも $\bigg\lfloor\dfrac{n}{p}\bigg\rfloor+1$ 回しか割り切れないと分かります.
よって,約分の結果 $P(a,\,d,\,n)$ は $p$ で高々 $1$ 回しか割り切れないことが分かります.
素数 $p$ が $\sqrt[3]{n}\lt p\leqq\sqrt{n}$ をみたすとき,$\dfrac{n}{p^3}\lt 1\leqq\dfrac{n}{p^2}$ とルジャンドルの定理より,$n!$ は $p$ でちょうど $\bigg\lfloor\dfrac{n}{p}\bigg\rfloor+\bigg\lfloor\dfrac{n}{p^2}\bigg\rfloor$ 回割り切れます.
$(\ast\ast)$ の中で,$p$ で割り切れるものは,上と同様の議論により高々 $\bigg\lfloor\dfrac{n}{p}\bigg\rfloor+1$ 個の項です.
$(\ast\ast)$ の中で,$p^2$ で割り切れるものも同様に,高々 $\bigg\lfloor\dfrac{n}{p^2}\bigg\rfloor+1$ 個の項です.
$p^3\gt n$ より,$(\ast\ast)$ に $p^3$ で割り切れる項はありません.
よって,$P(a,\,d,\,n)$ の分子は,$p$ で最大でも$\bigg\lfloor\dfrac{n}{p}\bigg\rfloor+\bigg\lfloor\dfrac{n}{p^2}\bigg\rfloor+2$ 回しか割り切れないと分かります.
よって,約分の結果 $P(a,\,d,\,n)$ は $p$ で高々 $2$ 回しか割り切れないことが分かります.
素数 $p$ が $\sqrt[\alpha+1]{n}\lt p\leqq\sqrt[\alpha]{n}$ をみたすとき,$\dfrac{n}{p^{\alpha+1}}\lt 1\leqq\dfrac{n}{p^\alpha}$ とルジャンドルの定理より,$n!$ は $p$ でちょうど
$(\ast\ast)$ の中で,$p$ で割り切れるものは高々 $\bigg\lfloor\dfrac{n}{p}\bigg\rfloor+1$ 個,
$p^2$ で割り切れるものは高々 $\bigg\lfloor\dfrac{n}{p^2}\bigg\rfloor+1$ 個,
以下同様に続けていき,$p^\alpha$ で割り切れるものは高々 $\bigg\lfloor\dfrac{n}{p^\alpha}\bigg\rfloor+1$ 個です.
$p^{\alpha+1}\gt n$ より,$(\ast\ast)$ に $p^{\alpha+1}$ で割り切れる項はありません.
よって,$P(a,\,d,\,n)$ の分子は,$p$ で最大でも
よって,約分の結果 $P(a,\,d,\,n)$ は $p$ で高々 $\alpha$ 回しか割り切れないことが分かります.
$n\leqq 2^m$ をみたす最小の整数 $m$ をとります.
$\sqrt[m+1]{n}\lt p\leqq\sqrt[m]{n}\leqq 2$ をみたす素数 $p$ は存在しないか,あったとしても $2$ だけです.
以上のような素数の探索は $m$ 回で終了し,ここで打ち切りにしてもOKということです!
以上により,$P(a,\,d,\,n)$ は,
$\sqrt{n}\lt p\leqq n$ をみたす素数では高々 $1$ 回,
$\sqrt[3]{n}\lt p\leqq\sqrt{n}$ をみたす素数では高々 $2$ 回,
$\qquad\vdots$
$\sqrt[\alpha+1]{n}\lt p\leqq\sqrt[\alpha]{n}$ をみたす素数では高々 $\alpha$ 回,
$\qquad\vdots$
$\sqrt[m+1]{n}\lt p\leqq\sqrt[m]{n}$ をみたす素数では高々 $m$ 回,
割り切れることが分かりました.
$P(a,\,d,\,n)$ の分子・分母に登場する可能性のある素因数はすべて登場しているので,
補題2につなげるために,右辺の積の順序を入れ替えます:
これでやっと伏線が回収できます^^
補題1,補題2より,
一方で,$d\geqq 4$ より,
すなわち,補題3の成立が示されました.
証明すべきことは,
補題3より,
ここで,$\alpha$ は最大のものを選ぶと約束しておきます.すなわち,$p^{\alpha+1}$ で割り切れる項はない,としておきます.
$p^\alpha$ で切れるもので最小の項を $a+kd=p^\alpha x\,\,(1\leqq k\leqq n)$ とします.
ここで,$d$ が $p$ で割り切れるとすると,$a=p^\alpha x-kd$ より,$a$ も $p$ で割り切れることになり,$a$ と $d$ が互いに素であることに反します.よって,$d$ は $p$ で割り切れません.
また,$a$ が $p^\alpha$ で割り切れるとすると,$kd=p^\alpha x-a$ より,$kd$ も $p^\alpha$ で割り切れることになりますが,$d$ が $p$ で割り切れないことと,$1\leqq k\leqq n\lt p^\alpha$ より,それは不可能です.よって,$a$ は $p^\alpha$ で割り切れません.
$a+kd$ 以外に $p^\alpha$ で割り切れる項があったとして,それを $a+ld=p^\alpha y\,\,(k\lt l)$ とします.
$a$,$a+d$,$\cdots$,$a+nd$ の最小公倍数を $L$ とします.$L$ は $p$ でちょうど $\alpha$ 回割り切れます.
一方右辺において,項はすべて整数であり,$\dfrac{L}{a+kd}$ 以外の項については,分子 $L$ は $p$ で $\alpha$ 回割り切れ,分母は $p$ で $\alpha-1$ 回以下しか割り切れないのですべて $p$ の倍数になります.
$\dfrac{L}{a+kd}$ のみ,分子・分母がともに $p$ でちょうど $\alpha$ 回割り切れるので $p$ の倍数になりません.
すなわち,左辺は $p$ の倍数だけど,右辺は $p$ の倍数ではありません.矛盾です!
以上により,$d\geqq 4$ のとき,$S(a,\,d,\,n)$ は整数にならないことが示されました.
これで,定理3の証明は完成です!!
お疲れ様でした~^^
いくらでも大きくなるのに,無数に存在する整数の値をすべて避けながら大きくなっていくというのは,なんとも不思議ですね^^!
この記事で解説した定理3の証明は,参考文献[3]の証明が元になっています.
ただし証明をいくつかの補題に分割し,証明の順序や一部の記号を変更しました.
最初,「そこまで難しくないだろう」と軽い気持ちで定理3の証明を調べ始めたのですが,文献[3]の証明は想像以上に技巧的で,著者のエルデシュの天才ぶりに感動しっぱなしでした^^!
この記事を通して数学に興味をもってくれる方が増えるのはもちろん嬉しいことですが,「長年定理3の証明を知りたかったけど,この記事を読んで初めて知ることができた」という方が現れてくれたら,最高に嬉しいです!!
参考文献
[1] Theisinger, L., "Bemerkung über die harmonische Reihe", Monatshefte für Mathematik und Physik, vol. 26 (1915), pp. 132--134.
[2] Kürschák, J., "A harmonikus sorról", Mathematikai és Fizikai Lapok, vol. 27 (1918), pp. 299--300.
[3] Erdős, P., "Egy Kürschák-féle elemi számelméleti tétel általánosítása", Matematikai és Fizikai Lapok, vol. 39 (1932), pp. 17--24.
定理3の結果だけは知っていたのですが,証明したことはなかったので,この度証明を追ってみることにしました!
追っていくうちに,「これはTwitterでは余白が狭すぎる」と感じたので(笑)ブログの記事にすることにしました.
証明に入る前に記号を定めておきます.
正の整数 $a$,$d$,$n$ に対し,
\[ S(a,\,d,\,n)=\sum_{k=0}^{n}\dfrac{1}{a+kd}=\dfrac{1}{a}+\dfrac{1}{a+d}+\cdots+\dfrac{1}{a+nd} \]
と定義します.また,$a$ と $d$ が互いに素でないとき,$g=\gcd(a,\,d)$ とすると,$a=ga^\prime$,$d=gd^\prime$,$\gcd(a^\prime,\,d^\prime)=1$ と表わされるので,
\begin{align*}
S(a,\,d,\,n)&=\sum_{k=0}^{n}\dfrac{1}{a+kd}=\sum_{k=0}^{n}\dfrac{1}{ga^\prime +kgd^\prime}\\
&=\sum_{k=0}^{n}\dfrac{1}{g(a^\prime+kd^\prime)}=\dfrac{1}{g}\sum_{k=0}^{n}\dfrac{1}{a^\prime+kd^\prime}=\dfrac{1}{g}S(a^\prime,\,d^\prime,\,n)
\end{align*}
となり,$S(a^\prime,\,d^\prime,\,n)$ が整数ではないとき,$S(a,\,d,\,n)$ も整数になりません.すなわち,$a$ と $d$ が互いに素である場合に$S(a,\,d,\,n)$ が整数にならないことが証明できれば,それ以外の場合にも証明ができたことになります.よって以下の証明において,$\boldsymbol{a}$ と $\boldsymbol{d}$ は互いに素であると仮定します.
また,$a\gt n$ とすると,
\[
0\lt S(a,\,d,\,n)=\dfrac{1}{a}+\dfrac{1}{a+d}+\cdots+\dfrac{1}{a+nd}
\lt\underbrace{\dfrac{1}{a}+\dfrac{1}{a}+\cdots+\dfrac{1}{a}}_{\text{$n+1$ 個}}=\dfrac{n+1}{a}\leqq 1 \]
となって $S(a,\,d,\,n)$ は整数になりません.よって,$\boldsymbol{a\leqq n}$ も仮定します.
$\boldsymbol{d=1}$ のとき
この記事の後半でご紹介するメインの証明は,$d\geqq 4$ の場合にしか通用しません!なので,$d=1,\,2,\,3$ の場合は個別に証明する必要があります.
本節では $d=1$ の場合,すなわち定理2を証明しようと思います.
実は,$d=1$ の場合の証明は,あとで述べる $d$ が正の奇数の場合の証明に含まれているのですが,他の場合の証明に慣れるという意味も込めて,$d=1$ の場合の証明は個別に述べようと思います.
証明すべきことは,
\[ S(a,\,1,\,n)=\dfrac{1}{a}+\dfrac{1}{a+1}+\cdots+\dfrac{1}{a+n} \]
が整数にならないことです.他の場合の証明にも共通することですが,$a$,$a+1$,$\cdots$,$a+n$ の中で特別な素数の累乗を約数にもつ項の存在を示し,それを利用して証明していきます.
$d=1$ の場合は,素数 $2$ に注目します!
$a$,$a+1$,$\cdots$,$a+n$ の中に $2$ で割り切れる項が存在しますが,その中で最も多くの回数 $2$ で割り切れるもので最小の項を $a+k\,\,(0\leqq k\leqq n)$ とします.
\[ a+k=2^\alpha x\quad(\text{$x$ は奇数}) \]
と表わします.ここで,$\alpha$ は $2$ で割り切れる回数であり,$a+k$ の取り方から,$a$,$a+1$,$\cdots$,$a+n$ の中に $2$ で $\alpha +1$ 回割り切れるものは存在しません.次に,$2$ で $\alpha$ 回割り切れるものは $a+k$ 以外にないことを示します.
$a+k$ 以外に $2^\alpha$ で割り切れる項があるとして,それを
\[ a+l=2^\alpha y\quad(\text{$0\leqq k\lt l\leqq n$,$y$ は奇数}) \]
とします.$a+k\lt a+l$ より,$x\lt y$ であり,$x$,$y$ はともに奇数なので,
\[ x\lt 2z\lt y\quad(\text{$z$ は正の整数}) \]
をみたす偶数 $2z$ が存在します.このとき,
\[ a+k=2^\alpha x\lt 2^\alpha \cdot 2z=2^{\alpha+1}z\lt 2^\alpha y=a+l \]
より,$a+k$ と $a+l$ の間に $2$ で $\alpha +1$ 回割り切れる数 $2^{\alpha+1}z$ が存在することになりますが,これは $\alpha$ を $2$ で割り切れる最大回数にとったことに矛盾します!以上により,$a$,$a+1$,$\cdots$,$a+n$ の中で $2^\alpha$ で割り切れるものは $a+k$ だた1つであることが分かりました.
次に,$a$,$a+1$,$\cdots$,$a+n$ の最小公倍数を $L$ とします.$L$ は $2$ でちょうど $\alpha$ 回割り切れます.
\[ LS(a,\,1,\,n)=\dfrac{L}{a}+\dfrac{L}{a+1}+\cdots+\dfrac{L}{a+k}+\cdots+\dfrac{L}{a+n} \]
を考えます.もし,$S(a,\,1,\,n)$ が整数であったとすると,$L$ は偶数なので,左辺は偶数になります.一方右辺において,項はすべて整数であり,$\dfrac{L}{a+k}$ 以外の項については,分子 $L$ は $2$ で $\alpha$ 回割り切れ,分母は $2$ で $\alpha-1$ 回以下しか割り切れないのですべて偶数になります.
$\dfrac{L}{a+k}$ のみ,分子・分母がともに $2$ でちょうど $\alpha$ 回割り切れるので奇数になります.
偶数の和に1つだけ奇数を加えたものなので右辺は奇数になりますが,左辺は偶数だったのでこれは矛盾です!!
以上により,$S(a,\,1,\,n)$ は整数にならないことが示されました.
$\boldsymbol{d=2}$ のとき
次に $d=2$ の場合を見ていきましょう.$a$ と $d$ が互いに素である場合を考えればよいので,$a$ は奇数です.
\[ S(a,\,2,\,n)=\dfrac{1}{a}+\dfrac{1}{a+2}+\cdots+\dfrac{1}{a+2n} \]
が整数にならないことを示します.分母には,$a$ から $a+2n$ までのすべての奇数が現れます.
$a\leqq n$ より,
\[ a+2n\geqq a+2a=3a \]
で,$3a$ は奇数なので,$a$,$a+2$,$\cdots$,$a+2n$ の中に,$3a$ と一致するものが存在します.$a$,$a+2$,$\cdots$,$a+2n$ の中に $3$ の倍数が存在することが分かったので,その中で最も多くの回数 $3$ で割り切れるもので最小の項を $a+2k\,\,(0\lt k\leqq n)$ とします.
\[ a+2k=3^\alpha x\quad(\text{$x$ は $3$ の倍数でない奇数}) \]
と表わします.ここで,$\alpha$ は $3$ で割り切れる回数であり,$a+2k$ の取り方から,$a$,$a+2$,$\cdots$,$a+2n$ の中に $3$ で $\alpha +1$ 回割り切れるものは存在しません.次に,$x=1$ であることを示します.
まず,$a\leqq 3^\alpha$ を示します.もし $3^\alpha\lt a$ であるとすると,$3^{\beta}\lt a$ をみたす最大の正整数 $\beta$ をとるとき,
\[ 3^\alpha\leqq 3^\beta\lt a\leqq 3^{\beta+1}\lt 3a\leqq a+2n \]
より,$a$,$a+2$,$\cdots$,$a+2n$ の中に $3$ で $\beta+1\,(\gt\alpha)$ 回割り切れる項が存在することになり $\alpha$ の最大性に矛盾します.よって,$a\leqq 3^\alpha$ です.また,$a+2n\lt 3^\alpha$ とすると,$a$,$a+2$,$\cdots$,$a+2n$ の中に $3^\alpha$ で割り切れるものが存在しなくなり $\alpha$ の選び方に反するので,$3^\alpha \leqq a+2n$ です.
よって,$a$,$a+2$,$\cdots$,$a+2n$ の中に $3^\alpha$ と一致するものが存在し,$k$ の選び方から,
\[ a+2k=3^\alpha\quad (\text{すなわち $x=1$}) \]
となることが分かります.$a$,$a+2$,$\cdots$,$a+2n$ の中に $3^\alpha$ で割り切れる項がもう1つあると仮定して,その項を
\[ a+2l=3^\alpha y\quad (\text{$0\leqq k\lt l\leqq n$,$y$ は $3$ の倍数でない奇数}) \]
と表わすと,$1\lt 3\lt 5\leqq y$ より,
\[ a+2k=3^\alpha<3^\alpha\cdot 3=3^{\alpha+1}<3^{\alpha}y=a+2l \]
となって,$3$ で $\alpha+1$ 回割り切れる項が存在することになって矛盾が生じます.よって,$a$,$a+2$,$\cdots$,$a+2n$ の中で $3$ で $\alpha$ 回割り切れるものは $a+2k$ のみであり,他の項は $3$ で $\alpha-1$ 回以下しか割り切れないことが分かりました.
$a$,$a+2$,$\cdots$,$a+2n$ の最小公倍数を $L$ とします.$L$ は $3$ でちょうど $\alpha$ 回割り切れます.
$S(a,\,2,\,n)$ が整数であると仮定して,
\[ LS(a,\,2,\,n)=\dfrac{L}{a}+\dfrac{L}{a+2}+\cdots+\dfrac{L}{a+2k}+\cdots+\dfrac{L}{a+2n} \]
を考えます.$L$ は $3$ の倍数なので,左辺は $3$ の倍数になります.一方右辺において,項はすべて整数であり,$\dfrac{L}{a+2k}$ 以外の項については,分子 $L$ は $3$ で $\alpha$ 回割り切れ,分母は $3$ で $\alpha-1$ 回以下しか割り切れないのですべて $3$ の倍数になります.
$\dfrac{L}{a+2k}$ のみ,分子・分母がともに $3$ でちょうど $\alpha$ 回割り切れるので $3$ の倍数になりません.
よって右辺は $3$ の倍数になりませんが,左辺は $3$ の倍数だったのでこれは矛盾です!!
以上により,$S(a,\,2,\,n)$ は整数にならないことが示されました.
$\boldsymbol{d=3}$ のとき
次に $d=3$ の場合を示すのですが,$d=1$ の場合と同様に,$2$ で割り切れる回数に注目すると,$d$ が正の奇数の場合の一般的な証明ができてしまいます.本節では $d=3$ の場合の証明にかえて,$d$ が正の奇数の場合の証明をご紹介します.以下,$d$ は正の奇数であるとします.
証明すべきことは,
\[ S(a,\,d,\,n)=\dfrac{1}{a}+\dfrac{1}{a+d}+\cdots+\dfrac{1}{a+nd} \]
が整数にならないことです.$a$,$a+d$,$\cdots$,$a+nd$ の中に $2$ で割り切れる項が存在しますが,その中で最も多くの回数 $2$ で割り切れるもので最小の項を $a+kd\,\,(0\leqq k\leqq n)$ とします.
\[ a+kd=2^\alpha x\quad(\text{$x$ は奇数}) \]
と表わします.$a+kd$ の取り方から,$a$,$a+d$,$\cdots$,$a+nd$ の中に $2$ で $\alpha +1$ 回割り切れるものは存在しません.次に,$a+kd$ 以外に $2^\alpha$ で割り切れる項が複数あるとして,それらの中で2番目に小さい項を,
\[ a+ld=2^\alpha y\quad(\text{$0\leqq k\lt l\leqq n$,$y$ は奇数}) \]
とします.このとき,
\[ (a+ld)-(a+kd)=(l-k)d=2^\alpha (y-x) \]
であり,$x$ と $y$ は奇数なので,$y-x$ は偶数になり,右辺は $2^{\alpha+1}$ の倍数になります.$d$ は奇数なので,$l-k\gt 0$ は $2^{\alpha+1}$ の倍数となり,$l-k\geqq 2^{\alpha+1}$ となります.ここで,
\[ k\lt k+2^\alpha\lt k+2^{\alpha+1}\leqq l \]
より,
\[ a+kd\lt a+(k+2^\alpha)d=2^\alpha(x+d)\lt a+ld \]
となり,$a+kd$ と $a+ld$ の間に $2^\alpha$ で割り切れる項があることが分かります.$a+ld$ は $2^\alpha$ で割り切れる2番目の項としてとったのでこれは矛盾です.以上により,$a$,$a+d$,$\cdots$,$a+nd$ の中で $2^\alpha$ で割り切れるものは $a+kd$ だた1つであることが分かりました.
次に,$a$,$a+d$,$\cdots$,$a+nd$ の最小公倍数を $L$ とします.$L$ は $2$ でちょうど $\alpha$ 回割り切れます.
\[ LS(a,\,d,\,n)=\dfrac{L}{a}+\dfrac{L}{a+d}+\cdots+\dfrac{L}{a+kd}+\cdots+\dfrac{L}{a+nd} \]
を考えます.もし,$S(a,\,d,\,n)$ が整数であったとすると,$L$ は偶数なので,左辺は偶数になります.一方右辺において,項はすべて整数であり,$\dfrac{L}{a+kd}$ 以外の項については,分子 $L$ は $2$ で $\alpha$ 回割り切れ,分母は $2$ で $\alpha-1$ 回以下しか割り切れないのですべて偶数になります.
$\dfrac{L}{a+kd}$ のみ,分子・分母がともに $2$ でちょうど $\alpha$ 回割り切れるので奇数になります.
すなわち,左辺は偶数,右辺は奇数となり矛盾を得ました!
以上により,$d$ が正の奇数のとき,$S(a,\,d,\,n)$ は整数にならないことが示されました.
補題1
ここまで,$d=1$ の場合,$d=2$ の場合,$d$ が正の奇数の場合を証明しました.いよいよメインの $d\geqq 4$ の場合の証明に入りましょう!
本節では,証明に必要な補題の1つを証明します.
補題の主張を述べるために,記号を用意します.
正の整数 $n$ と $0\leqq k\leqq n$ をみたす整数 $k$ に対し,二項係数 $\dbinom{n}{k}$ を
\[ \dbinom{n}{k}=\dfrac{n!}{k!(n-k)!} \]
で定義します.高校数学では,${}_n\mathrm{C}_k$ という記号の方が主流ですね^^次に,実数 $x$ に対し,$x\geqq n$ をみたす最大の整数 $n$ を $\lfloor x\rfloor$ で表します.例えば,$\lfloor 2\rfloor=2$,$\lfloor \pi\rfloor=3$ です.これも高校数学では,ガウス記号 $[x]$ で表わすのが主流ですね!
また,実数 $x$ に対し,$x\leqq n$ をみたす最小の整数 $n$ を $\lceil x\rceil$ で表します.例えば,$\lceil 2\rceil=2$,$\lceil \pi\rceil=4$ です.
以上で記号の準備が整ったので,補題1の主張を述べましょう:
補題1
正の整数 $n$ に対し,$m$ を $n\leqq 2^m$ をみたす最小の整数とする.数列 $a_1$,$a_2$,$\cdots$,$a_m$ を,
\[ a_1=\bigg\lceil\dfrac{n}{2}\bigg\rceil,\quad a_2=\bigg\lceil\dfrac{n}{2^2}\bigg\rceil,\quad\cdots\quad a_k=\bigg\lceil\dfrac{n}{2^k}\bigg\rceil,\quad\cdots\quad a_m=\bigg\lceil\dfrac{n}{2^m}\bigg\rceil \]
と定義する.このとき,
\[ \dbinom{2a_1}{a_1}\cdot\dbinom{2a_2}{a_2}\cdot\cdots\cdot\dbinom{2a_m}{a_m}\lt 4^n \]
が成り立つ.
証明は数学的帰納法で行いますが,$n\leqq 10$ の場合は個別に示す必要があります.
補題1の「感じ」をつかむために,$n=10$ の場合を計算してみます.
$n=10$ のとき,$2^3\lt 10\leqq 2^4$ より $m=4$ で,
\[ a_1=\bigg\lceil\dfrac{10}{2}\bigg\rceil=5,\quad a_2=\bigg\lceil\dfrac{10}{2^2}\bigg\rceil=3,\quad a_3=\bigg\lceil\dfrac{10}{2^3}\bigg\rceil=2,\quad a_4=\bigg\lceil\dfrac{10}{2^4}\bigg\rceil=1 \]
となるので,
\[ \dbinom{10}{5}\cdot\dbinom{6}{3}\cdot\dbinom{4}{2}\cdot\dbinom{2}{1}=252\cdot 20\cdot6\cdot2=60480\lt 1048576=4^{10} \]
となり,確かに成り立っています.$n\leqq 9$ の場合も同様にして示せます:
\begin{align*}
n=1:\quad & \dbinom{2}{1}=2\lt 4=4^{1}\\
n=2:\quad & \dbinom{2}{1}=2\lt 16=4^{2}\\
n=3:\quad & \dbinom{4}{2}\cdot\dbinom{2}{1}=2\cdot 6=12\lt 64=4^{3}\\
n=4:\quad & \dbinom{4}{2}\cdot\dbinom{2}{1}=2\cdot 6=12\lt 256=4^{4}\\
n=5:\quad & \dbinom{6}{3}\cdot\dbinom{4}{2}\cdot\dbinom{2}{1}=20\cdot 6\cdot 2=240\lt 1024=4^{5}\\
n=6:\quad & \dbinom{6}{3}\cdot\dbinom{4}{2}\cdot\dbinom{2}{1}=20\cdot 6\cdot 2=240\lt 4096=4^{6}\\
n=7:\quad & \dbinom{8}{4}\cdot\dbinom{4}{2}\cdot\dbinom{2}{1}=70\cdot 6\cdot 2=840\lt 16384=4^{7}\\
n=8:\quad & \dbinom{8}{4}\cdot\dbinom{4}{2}\cdot\dbinom{2}{1}=70\cdot 6\cdot 2=840\lt 65536=4^{8}\\
n=9:\quad & \dbinom{10}{5}\cdot\dbinom{6}{3}\cdot\dbinom{4}{2}\cdot\dbinom{2}{1}=252\cdot 20\cdot 6\cdot 2=60480\lt 262144=4^{9}\\
\end{align*}
上の計算のように,$n$ の値を固定すると,そこから $m$,$a_1$,$\cdots$,$a_m$ の値が決まります.以下の帰納法による証明において,$n$ 値を変えると別の数列が得られることに注意してください.帰納法による証明に入る前に,1つ補題を準備します:
補題A
$n\geqq 5$ のとき,$\dbinom{2n}{n}<4^{n-1}$ が成り立つ.
$n=5$ のとき,
\[ \dbinom{10}{5}=252<256=4^4 \]
より成り立ちます.ある $n\geqq 5$ での成立を仮定すると,
\begin{align*}
\dbinom{2(n+1)}{n+1}&=\dfrac{(2(n+1))!}{((n+1)!)^2}=\dfrac{(2n+2)(2n+1)(2n)!}{(n+1)^2(n!)^2}\\
&=\bigg(4-\dfrac{2}{n+1}\bigg)\dbinom{2n}{n}\lt 4\cdot 4^{n-1}=4^n
\end{align*}
より $n+1$ での成立も確認できます.数学的帰納法により,補題Aが示されました.
準備が整ったので証明に入りましょう!
$n\leqq 10$ の場合は既に示したので,$n\geqq 11$ とし,$n$ より小さい正の整数に対しては補題1が成り立っていると仮定します(このとき,$m\geqq 4$ です).
我々の目標は,
\[ \dbinom{2a_1}{a_1}\cdot\dbinom{2a_2}{a_2}\cdot\cdots\cdot\dbinom{2a_m}{a_m}\lt 4^n \]
を示すことです.ここで,$2a_2-1$に注目します.$a_2=\bigg\lceil\dfrac{n}{2^2}\bigg\rceil$より,$\dfrac{n}{2^2}\leqq a_2\lt\dfrac{n}{2^2}+1$ なので,
\[ 0<\dfrac{n}{2}-1\leqq 2a_2-1\lt\dfrac{n}{2}+1\lt n \]
であり,$2a_2-1$ は $n$ より小さい正の整数だと分かるので,$2a_2-1$ に対して補題1を適用することができます.すなわち,$l$ を $2a_2-1\leqq 2^l$ をみたす最小の整数とし,
\[ b_1=\bigg\lceil\dfrac{2a_2-1}{2}\bigg\rceil,\quad b_2=\bigg\lceil\dfrac{2a_2-1}{2^2}\bigg\rceil,\quad\cdots\quad b_l=\bigg\lceil\dfrac{2a_2-1}{2^l}\bigg\rceil \]
と定義するとき,
\[ \dbinom{2b_1}{b_1}\cdot\dbinom{2b_2}{b_2}\cdot\cdots\cdot\dbinom{2b_l}{b_l}\lt 4^{2a_2-1} \]
が成り立ちます.$a_1$,$a_2$,$\cdots$,$a_m$ と $b_1$,$b_2$,$\cdots$,$b_l$ の間の関係を調べましょう.
$2^{m-1}\lt n\leqq 2^m$ より,$2^{m-3}+1\leqq a_2=\bigg\lceil\dfrac{n}{4}\bigg\rceil\leqq 2^{m-2}$ なので,
\[ 2^{m-2}\lt 2^{m-2}+1\leqq 2a_2-1\leqq2^{m-1}-1\lt 2^{m-1} \]
であり,$l=m-1$ だと分かります.また,
\[ b_1=\bigg\lceil\dfrac{2a_2-1}{2}\bigg\rceil=\bigg\lceil a_2-\dfrac{1}{2}\bigg\rceil=a_2 \]
です.$2\leqq k\leqq l$ に対しても,$b_k=a_{k+1}$ が成り立つことを示します.
そのために,$n=2^{k+1}q+r\,\,(0\leqq r\lt 2^{k+1})$ と表わして,$a_{k+1}$ と $b_k$ を計算します.
$r=0$ のとき,
\[ a_{k+1}=\bigg\lceil\dfrac{n}{2^{k+1}}\bigg\rceil=\bigg\lceil\dfrac{2^{k+1}q}{2^{k+1}}\bigg\rceil=q \]
であり,$a_2=\bigg\lceil\dfrac{2^{k+1}q}{2^2}\bigg\rceil=2^{k-1}q$ より,
\[ b_k=\bigg\lceil\dfrac{2a_2-1}{2^k}\bigg\rceil=\bigg\lceil\dfrac{2^k q-1}{2^k}\bigg\rceil=\bigg\lceil q-\dfrac{1}{2^k}\bigg\rceil=q \]
なので,$a_{k+1}=b_k$ です.$0\lt r\lt 2^{k+1}$ のとき,
\[ a_{k+1}=\bigg\lceil\dfrac{n}{2^{k+1}}\bigg\rceil=\bigg\lceil\dfrac{2^{k+1}q+r}{2^{k+1}}\bigg\rceil=\bigg\lceil q+\dfrac{r}{2^{k+1}}\bigg\rceil=q+1 \]
であり,$a_2=\bigg\lceil\dfrac{2^{k+1}q+r}{2^2}\bigg\rceil=2^{k-1}q+\bigg\lceil\dfrac{r}{4}\bigg\rceil$ および $1\leqq\bigg\lceil\dfrac{r}{4}\bigg\rceil\leqq 2^{k-1}$ より,
\[ b_k=\bigg\lceil\dfrac{2a_2-1}{2^k}\bigg\rceil=\bigg\lceil q+\dfrac{2\lceil r/4\rceil-1}{2^k}\bigg\rceil=q+1 \]
なので,$a_{k+1}=b_k$ です.以上により,
\[ a_2=b_1,\quad a_3=b_2,\quad \cdots\quad a_{m}=b_{m-1} \]
となることが示されました.また,$n\geqq 11$ より,$a_1=\bigg\lceil\dfrac{n}{2}\bigg\rceil\geqq 6$ なので,補題Aを $a_1$ に適用することができ,
\[ \dbinom{2a_1}{a_1}\lt 4^{a_1-1} \]
となることも分かります.よって,
\begin{align*}
\dbinom{2a_1}{a_1}\cdot\dbinom{2a_2}{a_2}\cdot\cdots\cdot\dbinom{2a_m}{a_m}&=\dbinom{2a_1}{a_1}\cdot\dbinom{2b_1}{b_1}\cdot\dbinom{2b_2}{b_2}\cdot\cdots\cdot\dbinom{2b_{m-1}}{b_{m-1}}\\[0.5em]
&\lt 4^{a_1-1}\cdot4^{2a_2-1}=4^{a_1+2a_2-2}
\end{align*}
が得られます.$a_1=\bigg\lceil\dfrac{n}{2}\bigg\rceil$,$a_2=\bigg\lceil\dfrac{n}{4}\bigg\rceil$ より,
\[ a_1+2a_2-2\lt\dfrac{n}{2}+1+2\bigg(\dfrac{n}{4}+1\bigg)-2=n+1 \]
で,$a_1$,$a_2$ は正の整数なので $a_1+2a_2-2\leqq n$ となるので,
\[ \dbinom{2a_1}{a_1}\cdot\dbinom{2a_2}{a_2}\cdot\cdots\cdot\dbinom{2a_m}{a_m}\lt 4^{n} \]
が示されました.補題1の証明終了です!!
補題2
前節に続き,本節でも定理3の証明に必要な補題を示します.その前に,また新たな記号を導入します.
積の記号 $\prod$ の左上にアスタリスクをつけた記号 $\sideset{^\ast}{}{\prod}$ で,素数のみの積をとる記号を表わすことにします.
ただし,条件に合う素数がないときは値が $1$ であると決めておきます.
例えば,
\[ \sideset{^\ast}{}{\prod}_{k\lt 10}k^2=2^2\cdot 3^2\cdot 5^2\cdot 7^2=44100,\quad \sideset{^\ast}{}{\prod}_{90\leqq n\leqq 96}n=1 \]
です.この記号を用いて,補題2は次のように述べられます:
補題2
正の整数 $n$ に対し,$m$,$a_1$,$a_2$,$\cdots$,$a_m$ は補題1で定めたものとする.このとき,
\[ \bigg(\sideset{^\ast}{}{\prod}_{k\leqq n}k\bigg)\cdot\bigg(\sideset{^\ast}{}{\prod}_{k\leqq\sqrt{n}}k\bigg)\cdot\cdots\cdot\bigg(\sideset{^\ast}{}{\prod}_{k\leqq\sqrt[m]{n}}k\bigg)\leqq\dbinom{2a_1}{a_1}\cdot\dbinom{2a_2}{a_2}\cdot\cdots\cdot\dbinom{2a_m}{a_m} \]
が成り立つ.
補題2の「感じ」をつかむために,$n=30$ の場合を計算してみましょう(あまり小さな数だと「感じ」がつかみにくいので^^;).
$n=30$ のとき,$2^4\lt 30\leqq 2^5$ より $m=5$ で,
\begin{align*}
&a_1=\bigg\lceil\dfrac{30}{2}\bigg\rceil=15,\quad a_2=\bigg\lceil\dfrac{30}{2^2}\bigg\rceil=8,\quad a_3=\bigg\lceil\dfrac{30}{2^3}\bigg\rceil=4,\\
&a_4=\bigg\lceil\dfrac{30}{2^4}\bigg\rceil=2,\quad a_5=\bigg\lceil\dfrac{30}{2^5}\bigg\rceil=1
\end{align*}
となります.左辺の積を1つ1つ見ると,
\begin{align*}
\sideset{^\ast}{}{\prod}_{k\leqq 30}k&=2\times 3\times 5\times 7\times 11\times 13\times 17\times 19\times 23\times 29\\
\sideset{^\ast}{}{\prod}_{k\leqq \sqrt{30}}k&=2\times 3\times 5\\
\sideset{^\ast}{}{\prod}_{k\leqq \sqrt[3]{30}}k&=2\times 3\\
\sideset{^\ast}{}{\prod}_{k\leqq \sqrt[4]{30}}k&=2\\
\sideset{^\ast}{}{\prod}_{k\leqq \sqrt[5]{30}}k&=1
\end{align*}
また,右辺の二項係数を1つ1つ見ると,
\begin{align*}
\dbinom{30}{15}&=2^4\times 3^2\times 5\times 17\times 19\times 23\times 29\\
\dbinom{16}{8}&=2\times 3^2\times 5\times 11\times 13\\
\dbinom{8}{4}&=2\times 5\times 7\\
\dbinom{4}{2}&=2\times 3\\
\dbinom{2}{1}&=2
\end{align*}
であり,確かにすべての素数について,左辺よりも右辺の方が多くの回数登場しているので,$\text{左辺}\leqq\text{右辺}$ は成立しています.ですが,このような単純に両辺の素数の個数を比較するような方法は,一般の $n$ の場合には適用できそうもありません.
そこで,区間を上手に分割して素数の数を比べるという方法をとります.
補題2の仮定のもとで,$\alpha$,$k$ を $1\leqq \alpha,\, k\leqq m$ をみたす整数とし,区間
\[ \lfloor\sqrt[\alpha]{a_k}\rfloor\lt x\leqq\lfloor\sqrt[\alpha]{2a_k}\rfloor \]
を考えます.このように定義した区間は,次の性質をもちます:
補題B
① $1\leqq\alpha\leqq m$ のとき,区間
\[ \lfloor\sqrt[\alpha]{a_m}\rfloor\lt x\leqq\lfloor\sqrt[\alpha]{2a_m}\rfloor,\, \lfloor\sqrt[\alpha]{a_{m-1}}\rfloor\lt x\leqq\lfloor\sqrt[\alpha]{2a_{m-1}}\rfloor,\,\cdots,\,\lfloor\sqrt[\alpha]{a_1}\rfloor\lt x\leqq\lfloor\sqrt[\alpha]{2a_1}\rfloor \]
は,区間 $1\lt x\leqq\sqrt[\alpha]{n}$ を隙間なく覆いつくす.② $1\leqq k\leqq m$ のとき,区間
\[ \lfloor\sqrt[m]{a_k}\rfloor\lt x\leqq\lfloor\sqrt[m]{2a_k}\rfloor,\,\cdots,\, \lfloor\sqrt{a_k}\rfloor\lt x\leqq\lfloor\sqrt{2a_k}\rfloor,\, a_k\lt x\leqq 2a_k \]
は共通部分をもたない.
\[ a_1=\bigg\lceil\dfrac{n}{2}\bigg\rceil,\quad a_2=\bigg\lceil\dfrac{n}{2^2}\bigg\rceil,\quad \cdots\quad a_m=\bigg\lceil\dfrac{n}{2^m}\bigg\rceil \]
という定義を思い出すと,
\[ a_1\geqq a_2\geqq\cdots\geqq a_m \]
は明らかです.$1\leqq k\leqq m-1$ とします.
\[ a_{k}=\bigg\lceil\dfrac{n}{2^{k}}\bigg\rceil\lt\dfrac{n}{2^k}+1=2\cdot\dfrac{n}{2^{k+1}}+1\leqq 2a_{k+1}+1 \]
であり,$a_k$ と $a_{k+1}$ はともに整数なので,
\[ a_k\leqq 2a_{k+1} \]
が成り立ちます.
\[ a_m=1,\quad 2a_1=2\cdot\bigg\lceil\dfrac{n}{2}\bigg\rceil\geqq 2\cdot\dfrac{n}{2}=n \]
であることも合わせると,$1\leqq \alpha\leqq m$ に対し,区間
\[ \lfloor\sqrt[\alpha]{a_m}\rfloor\lt x\leqq\lfloor\sqrt[\alpha]{2a_m}\rfloor,\, \lfloor\sqrt[\alpha]{a_{m-1}}\rfloor\lt x\leqq\lfloor\sqrt[\alpha]{2a_{m-1}}\rfloor,\,\cdots,\,\lfloor\sqrt[\alpha]{a_1}\rfloor\lt x\leqq\lfloor\sqrt[\alpha]{2a_1}\rfloor \]
は,区間 $1\lt x\leqq \sqrt[\alpha]{n}$ を覆いつくすことが分かります(共通部分は存在する場合があります).これで①は示されました.次に,$1\leqq k\leqq m$ を1つ固定して,$1\leqq \alpha\leqq m-1$ に対し,
\[ \lfloor\sqrt[\alpha+1]{a_k}\rfloor\lt x\leqq\lfloor\sqrt[\alpha+1]{2a_k}\rfloor,\quad \lfloor\sqrt[\alpha]{a_k}\rfloor\lt x\leqq\lfloor\sqrt[\alpha]{2a_k}\rfloor \]
が共通部分をもたないことを示します.もし,$1\leqq a_k\lt 2^\alpha$ だとすると,$\sqrt[\alpha+1]{2a_k}\lt 2$ なので,
\[ 1\leqq\lfloor\sqrt[\alpha+1]{a_k}\rfloor\leqq\lfloor\sqrt[\alpha+1]{2a_k}\rfloor=1\]
となり,区間
\[ \lfloor\sqrt[\alpha+1]{a_k}\rfloor\lt x\leqq\lfloor\sqrt[\alpha+1]{2a_k}\rfloor \]
は空集合になります.$a_k\geqq 2^\alpha$ だとすると,この不等式の両辺に $a_k{}^\alpha$ をかけて,
\[ 2^\alpha a_k{}^\alpha\leqq a_k{}^{\alpha+1}\quad\text{より,}\quad \sqrt[\alpha+1]{2a_k}\leqq\sqrt[\alpha]{a_k} \]
なので,$\lfloor\sqrt[\alpha+1]{2a_k}\rfloor\leqq\lfloor\sqrt[\alpha]{a_k}\rfloor$ であり,区間
\[ \lfloor\sqrt[\alpha+1]{a_k}\rfloor\lt x\leqq\lfloor\sqrt[\alpha+1]{2a_k}\rfloor,\quad \lfloor\sqrt[\alpha]{a_k}\rfloor\lt x\leqq\lfloor\sqrt[\alpha]{2a_k}\rfloor \]
は共通部分をもちません.これで②も示されました.以上で,補題Bの証明終了です!
補題Bに続けて,次の補題Cも示します:
補題C
$n$ と $\alpha$ を正の整数とする.素数 $p$ が
\[ \lfloor\sqrt[\alpha]{n}\rfloor\lt p\leqq\lfloor\sqrt[\alpha]{2n}\rfloor \]
をみたすとき,二項係数 $\dbinom{2n}{n}=\dfrac{(2n)!}{(n!)^2}$ は $p$ で割り切れる.
ルジャンドルの定理
$n$ を正の整数,$p$ を素数とする.このとき,$n!$ が $p$ で割り切れる回数は,
\[ \bigg\lfloor\dfrac{n}{p}\bigg\rfloor+\bigg\lfloor\dfrac{n}{p^2}\bigg\rfloor+\bigg\lfloor\dfrac{n}{p^3}\bigg\rfloor+\cdots \]
である.
いま,$\lfloor\sqrt[\alpha]{n}\rfloor\lt p\leqq\lfloor\sqrt[\alpha]{2n}\rfloor$ であり,$p$ が整数であることから,$\sqrt[\alpha]{n}\lt p\leqq\sqrt[\alpha]{2n}$ なので,
\[ \dfrac{2n}{p^{\alpha+1}}\leqq\dfrac{n}{p^\alpha}\lt 1\leqq\dfrac{2n}{p^\alpha}\lt 2 \quad\text{より}\quad \bigg\lfloor\dfrac{n}{p^\alpha}\bigg\rfloor=0,\,\,\bigg\lfloor\dfrac{2n}{p^\alpha}\bigg\rfloor=1,\,\,\bigg\lfloor\dfrac{2n}{p^{\alpha+1}}\bigg\rfloor=0 \]
となります.よって,$(2n)!$ が $p$ で割り切れる回数は,
\[ \bigg\lfloor\dfrac{2n}{p}\bigg\rfloor+\bigg\lfloor\dfrac{2n}{p^2}\bigg\rfloor+\cdots+\bigg\lfloor\dfrac{2n}{p^{\alpha-1}}\bigg\rfloor+1 \]
であり,$n!$ が $p$ で割り切れる回数は,
\[ \bigg\lfloor\dfrac{n}{p}\bigg\rfloor+\bigg\lfloor\dfrac{n}{p^2}\bigg\rfloor+\cdots+\bigg\lfloor\dfrac{n}{p^{\alpha-1}}\bigg\rfloor \]
です.$\lfloor 2x\rfloor\geqq 2\lfloor x\rfloor$ であることも用いると,
\[ \bigg\lfloor\dfrac{2n}{p}\bigg\rfloor+\bigg\lfloor\dfrac{2n}{p^2}\bigg\rfloor+\cdots+\bigg\lfloor\dfrac{2n}{p^{\alpha-1}}\bigg\rfloor+1-2\bigg(\bigg\lfloor\dfrac{n}{p}\bigg\rfloor+\bigg\lfloor\dfrac{n}{p^2}\bigg\rfloor+\cdots+\bigg\lfloor\dfrac{n}{p^{\alpha-1}}\bigg\rfloor\bigg)\geqq 1 \]
であり,分子が分母よりも1回以上多く $p$ で割り切れます.よって,二項係数 $\dbinom{2n}{n}$ は $p$ で割り切れることが示されました.
以上の2つの補題を用いて,補題2の不等式
\[ \bigg(\sideset{^\ast}{}{\prod}_{k\leqq n}k\bigg)\cdot\bigg(\sideset{^\ast}{}{\prod}_{k\leqq\sqrt{n}}k\bigg)\cdot\cdots\cdot\bigg(\sideset{^\ast}{}{\prod}_{k\leqq\sqrt[m]{n}}k\bigg)\leqq\dbinom{2a_1}{a_1}\cdot\dbinom{2a_2}{a_2}\cdot\cdots\cdot\dbinom{2a_m}{a_m}\qquad\cdots\cdots\,(\ast) \]
を示します.証明の方針としては,左辺の素因数が,常に右辺の素因数にもなっていることを示します.
左辺の素因数の1つを $p$ とします.$p$ はどこかの積のグループに含まれているので,その1つを
\[ \sideset{^\ast}{}{\prod}_{k\leqq\sqrt[\alpha]{n}}k\quad (1\leqq \alpha\leqq m) \]
とします.このとき,$p\leqq\sqrt[\alpha]{n}$ です.補題B①より,
\[ \lfloor\sqrt[\alpha]{a_m}\rfloor\lt x\leqq\lfloor\sqrt[\alpha]{2a_m}\rfloor,\, \lfloor\sqrt[\alpha]{a_{m-1}}\rfloor\lt x\leqq\lfloor\sqrt[\alpha]{2a_{m-1}}\rfloor,\,\cdots,\,\lfloor\sqrt[\alpha]{a_1}\rfloor\lt x\leqq\lfloor\sqrt[\alpha]{2a_1}\rfloor \]
は,区間 $1\lt x\leqq\sqrt[\alpha]{n}$ を隙間なく覆いつくしているので,素数 $p$ はどれかの区間に含まれます.$p$ を含む区間の1つを,$\lfloor\sqrt[\alpha]{a_k}\rfloor\lt x\leqq\lfloor\sqrt[\alpha]{2a_k}\rfloor$ とすると,補題Cにより,$\dbinom{2a_k}{a_k}$ は $p$ を素因数にもちます.
不等式 $(\ast)$ の左辺が素因数 $p$ を複数個もっている場合を考えます.
素因数 $p$ を2つもっている場合,その2つは異なる積のグループからとり出されているので,それらを,
\[ \sideset{^\ast}{}{\prod}_{k\leqq\sqrt[\alpha]{n}}k,\quad \sideset{^\ast}{}{\prod}_{k\leqq\sqrt[\beta]{n}}k\quad (1\leqq\alpha\lt\beta\leqq m) \]
とします.このとき,上と同様に,
\[ \lfloor\sqrt[\alpha]{a_k}\rfloor\lt p\leqq\lfloor\sqrt[\alpha]{2a_k}\rfloor,\quad \lfloor\sqrt[\beta]{a_l}\rfloor\lt p\leqq\lfloor\sqrt[\beta]{2a_l}\rfloor \]
をみたす区間をとることができます.もし,$a_k=a_l$であるとすると,区間
\[ \lfloor\sqrt[\alpha]{a_k}\rfloor\lt x\leqq\lfloor\sqrt[\alpha]{2a_k}\rfloor,\quad \lfloor\sqrt[\beta]{a_k}\rfloor\lt x\leqq\lfloor\sqrt[\beta]{2a_k}\rfloor \]
が共通な要素 $p$ をもつことになり,共通部分をもたないという補題B②に矛盾します.よって,$a_k\neq a_l$ であり,$\dbinom{2a_k}{a_k}$,$\dbinom{2a_l}{a_l}$ がともに $p$ を素因数にもちます.
このように,$(\ast)$ の左辺が $p$ で割り切れる回数に応じて,右辺で $p$ で割り切れる二項係数を選び出すことができます.
これは,不等式 $(\ast)$ が成り立つことを示しており,補題2が証明されました!
補題3
ここまで,2つの節にわたり補題を準備してきました.本節では,$d\geqq 4$ の場合の証明のための最後の補題を準備します:
補題3
$a$,$n$ を正の整数とし,$d$ を $d\geqq 4$ をみたす整数とする.このとき,素数 $p$ と正の整数 $\alpha$ で,$p^\alpha\gt n$ かつ,
\[ a+d,\quad a+2d,\quad\cdots\quad a+nd \]
のいずれかが $p^\alpha$ で割り切れるようなものが存在する.
\[ a+d,\quad a+2d,\quad\cdots\quad a+nd \qquad\cdots\cdots\,(\ast\ast) \]
のすべての項が,$p^\alpha\leqq n$ をみたす素数の累乗でしか割り切れないと仮定します.矛盾を導くために,
\[ P(a,\,d,\,n)=\dfrac{(a+d)(a+2d)\cdots(a+nd)}{n!} \]
という式を考え,この式を上から評価します.分子と分母が素数で割り切れる回数を比較し,約分の結果残されるものを数えます.上からの評価が得られればよいので,分子の方は多めに見積もってもよいことに注意してください.ここで,$p$ を素数として,$(\ast\ast)$ の中に $p$ で割り切れる項 $a+kd$ が存在するとします.このとき,$d$ は $p$ で割り切れません.もし $d$ が $p$ で割り切れるとすると,$a$ も $p$ で割り切れることになり,$a$ と $d$ が互いに素であるという条件に反するからです.
素数 $p$ が $p\gt n$ をみたすとき,仮定により $(\ast\ast)$ の中に $p$ で割り切れる項はありません.もちろん $n!$ も割り切れません.
素数 $p$ が $\sqrt{n}\lt p\leqq n$ をみたすとき,$\dfrac{n}{p^2}\lt 1\leqq\dfrac{n}{p}$ とルジャンドルの定理より,$n!$ は $p$ でちょうど $\bigg\lfloor\dfrac{n}{p}\bigg\rfloor$ 回割り切れます.
$(\ast\ast)$ の中で,$p$ で割り切れるものが存在するとして,その中で最小のものを $a+k_1d=px$,2番目に小さいものを $a+k_2d=py$ とします.差をとると,
\[ (a+k_2d)-(a+k_1d)=(k_2-k_1)d=p(y-x) \]
であり,$d$ が $p$ で割り切れないことから,$k_2-k_1$ は $p$ の倍数であることが分かります.
\[ a+(k_1+p)d=a+k_1d+pd=px+pd=p(x+d) \]
より,$k_2=k_1+p$ です.以上の考察から,$(\ast\ast)$ の中で $p$ で割り切れるものは,
\[ a+k_1d,\quad a+(k_1+p)d,\quad a+(k_1+2p)d,\quad\cdots\cdots \]
に限られ,$p$ で割り切れるものは,高々 $\bigg\lfloor\dfrac{n}{p}\bigg\rfloor+1$ 個の項であることが分かります.$p^2\gt n$ より,$(\ast\ast)$ に $p^2$ で割り切れる項はないので,$P(a,\,d,\,n)$ の分子は,$p$ で最大でも $\bigg\lfloor\dfrac{n}{p}\bigg\rfloor+1$ 回しか割り切れないと分かります.
よって,約分の結果 $P(a,\,d,\,n)$ は $p$ で高々 $1$ 回しか割り切れないことが分かります.
素数 $p$ が $\sqrt[3]{n}\lt p\leqq\sqrt{n}$ をみたすとき,$\dfrac{n}{p^3}\lt 1\leqq\dfrac{n}{p^2}$ とルジャンドルの定理より,$n!$ は $p$ でちょうど $\bigg\lfloor\dfrac{n}{p}\bigg\rfloor+\bigg\lfloor\dfrac{n}{p^2}\bigg\rfloor$ 回割り切れます.
$(\ast\ast)$ の中で,$p$ で割り切れるものは,上と同様の議論により高々 $\bigg\lfloor\dfrac{n}{p}\bigg\rfloor+1$ 個の項です.
$(\ast\ast)$ の中で,$p^2$ で割り切れるものも同様に,高々 $\bigg\lfloor\dfrac{n}{p^2}\bigg\rfloor+1$ 個の項です.
$p^3\gt n$ より,$(\ast\ast)$ に $p^3$ で割り切れる項はありません.
よって,$P(a,\,d,\,n)$ の分子は,$p$ で最大でも$\bigg\lfloor\dfrac{n}{p}\bigg\rfloor+\bigg\lfloor\dfrac{n}{p^2}\bigg\rfloor+2$ 回しか割り切れないと分かります.
よって,約分の結果 $P(a,\,d,\,n)$ は $p$ で高々 $2$ 回しか割り切れないことが分かります.
素数 $p$ が $\sqrt[\alpha+1]{n}\lt p\leqq\sqrt[\alpha]{n}$ をみたすとき,$\dfrac{n}{p^{\alpha+1}}\lt 1\leqq\dfrac{n}{p^\alpha}$ とルジャンドルの定理より,$n!$ は $p$ でちょうど
\[ \bigg\lfloor\dfrac{n}{p}\bigg\rfloor+\bigg\lfloor\dfrac{n}{p^2}\bigg\rfloor+\cdots+\bigg\lfloor\dfrac{n}{p^\alpha}\bigg\rfloor \]
回割り切れます.$(\ast\ast)$ の中で,$p$ で割り切れるものは高々 $\bigg\lfloor\dfrac{n}{p}\bigg\rfloor+1$ 個,
$p^2$ で割り切れるものは高々 $\bigg\lfloor\dfrac{n}{p^2}\bigg\rfloor+1$ 個,
以下同様に続けていき,$p^\alpha$ で割り切れるものは高々 $\bigg\lfloor\dfrac{n}{p^\alpha}\bigg\rfloor+1$ 個です.
$p^{\alpha+1}\gt n$ より,$(\ast\ast)$ に $p^{\alpha+1}$ で割り切れる項はありません.
よって,$P(a,\,d,\,n)$ の分子は,$p$ で最大でも
\[ \bigg\lfloor\dfrac{n}{p}\bigg\rfloor+\bigg\lfloor\dfrac{n}{p^2}\bigg\rfloor+\cdots+\bigg\lfloor\dfrac{n}{p^\alpha}\bigg\rfloor+\alpha \]
回しか割り切れないと分かります.よって,約分の結果 $P(a,\,d,\,n)$ は $p$ で高々 $\alpha$ 回しか割り切れないことが分かります.
$n\leqq 2^m$ をみたす最小の整数 $m$ をとります.
$\sqrt[m+1]{n}\lt p\leqq\sqrt[m]{n}\leqq 2$ をみたす素数 $p$ は存在しないか,あったとしても $2$ だけです.
以上のような素数の探索は $m$ 回で終了し,ここで打ち切りにしてもOKということです!
以上により,$P(a,\,d,\,n)$ は,
$\sqrt{n}\lt p\leqq n$ をみたす素数では高々 $1$ 回,
$\sqrt[3]{n}\lt p\leqq\sqrt{n}$ をみたす素数では高々 $2$ 回,
$\qquad\vdots$
$\sqrt[\alpha+1]{n}\lt p\leqq\sqrt[\alpha]{n}$ をみたす素数では高々 $\alpha$ 回,
$\qquad\vdots$
$\sqrt[m+1]{n}\lt p\leqq\sqrt[m]{n}$ をみたす素数では高々 $m$ 回,
割り切れることが分かりました.
$P(a,\,d,\,n)$ の分子・分母に登場する可能性のある素因数はすべて登場しているので,
\[ P(a,\,d,\,n)\leqq\bigg(\sideset{^\ast}{}{\prod}_{\sqrt{n}\lt k\leqq n}k\bigg)\cdot\bigg(\sideset{^\ast}{}{\prod}_{\sqrt[3]{n}\lt k\leqq\sqrt{n}}k^2\bigg)\cdot\cdots\cdot\bigg(\sideset{^\ast}{}{\prod}_{\sqrt[m+1]{n}\lt k\leqq\sqrt[m]{n}}k^m\bigg) \]
という評価が得られます.補題2につなげるために,右辺の積の順序を入れ替えます:
\begin{align*}
&\bigg(\sideset{^\ast}{}{\prod}_{\sqrt[m+1]{n}\lt k\leqq\sqrt[m]{n}}k^m\bigg)\cdot\bigg(\sideset{^\ast}{}{\prod}_{\sqrt[m]{n}\lt k\leqq\sqrt[m-1]{n}}k^{m-1}\bigg)\cdot\cdots\cdot\bigg(\sideset{^\ast}{}{\prod}_{\sqrt[3]{n}\lt k\leqq\sqrt{n}}k^2\bigg)\cdot\bigg(\sideset{^\ast}{}{\prod}_{\sqrt{n}\lt k\leqq n}k\bigg)\\
=&\bigg(\sideset{^\ast}{}{\prod}_{\sqrt[m+1]{n}\lt k\leqq\sqrt[m]{n}}k\bigg)\cdot\bigg(\sideset{^\ast}{}{\prod}_{\sqrt[m]{n}\lt k\leqq\sqrt[m-1]{n}}k\bigg)\cdot\cdots\cdot\bigg(\sideset{^\ast}{}{\prod}_{\sqrt[3]{n}\lt k\leqq\sqrt{n}}k\bigg)\cdot\bigg(\sideset{^\ast}{}{\prod}_{\sqrt{n}\lt k\leqq n}k\bigg)\cdot\\
&\bigg(\sideset{^\ast}{}{\prod}_{\sqrt[m+1]{n}\lt k\leqq\sqrt[m]{n}}k\bigg)\cdot\bigg(\sideset{^\ast}{}{\prod}_{\sqrt[m]{n}\lt k\leqq\sqrt[m-1]{n}}k\bigg)\cdot\cdots\cdot\bigg(\sideset{^\ast}{}{\prod}_{\sqrt[3]{n}\lt k\leqq\sqrt{n}}k\bigg)\cdot\\
&\quad\qquad\,\,\vdots\qquad\qquad\qquad\quad\vdots\\
&\bigg(\sideset{^\ast}{}{\prod}_{\sqrt[m+1]{n}\lt k\leqq\sqrt[m]{n}}k\bigg)\cdot\bigg(\sideset{^\ast}{}{\prod}_{\sqrt[m]{n}\lt k\leqq\sqrt[m-1]{n}}k\bigg)\cdot\\
&\bigg(\sideset{^\ast}{}{\prod}_{\sqrt[m+1]{n}\lt k\leqq\sqrt[m]{n}}k\bigg)\\
=&\bigg(\sideset{^\ast}{}{\prod}_{k\leqq n}k\bigg)\cdot\bigg(\sideset{^\ast}{}{\prod}_{k\leqq\sqrt{n}}k\bigg)\cdot\cdots\cdot\bigg(\sideset{^\ast}{}{\prod}_{k\leqq\sqrt[m-1]{n}}k\bigg)\cdot\bigg(\sideset{^\ast}{}{\prod}_{k\leqq\sqrt[m]{n}}k\bigg)
\end{align*}
なので,上の不等式は,
\[ P(a,\,d,\,n)\leqq\bigg(\sideset{^\ast}{}{\prod}_{k\leqq n}k\bigg)\cdot\bigg(\sideset{^\ast}{}{\prod}_{k\leqq\sqrt{n}}k\bigg)\cdot\cdots\cdot\bigg(\sideset{^\ast}{}{\prod}_{k\leqq\sqrt[m-1]{n}}k\bigg)\cdot\bigg(\sideset{^\ast}{}{\prod}_{k\leqq\sqrt[m]{n}}k\bigg) \]
と書きかえられます.これでやっと伏線が回収できます^^
補題1,補題2より,
\begin{align*}
P(a,\,d,\,n)&\leqq\bigg(\sideset{^\ast}{}{\prod}_{k\leqq n}k\bigg)\cdot\bigg(\sideset{^\ast}{}{\prod}_{k\leqq\sqrt{n}}k\bigg)\cdot\cdots\cdot\bigg(\sideset{^\ast}{}{\prod}_{k\leqq\sqrt[m]{n}}k\bigg)\\
&\leqq\dbinom{2a_1}{a_1}\cdot\dbinom{2a_2}{a_2}\cdot\cdots\cdot\dbinom{2a_m}{a_m}\lt 4^n
\end{align*}
が得られます.一方で,$d\geqq 4$ より,
\begin{align*}
P(a,\,d,\,n)&=\dfrac{(a+d)(a+2d)\cdots(a+nd)}{n!}\\
&=\bigg(\dfrac{a}{1}+d\bigg)\bigg(\dfrac{a}{2}+d\bigg)\cdots\bigg(\dfrac{a}{n}+d\bigg)\gt d^n\geqq 4^n
\end{align*}
となるので矛盾に達します!!すなわち,補題3の成立が示されました.
$\boldsymbol{d\geqq 4}$ のとき
補題3を利用して,$d\geqq 4$ の場合を証明します.証明すべきことは,
\[ S(a,\,d,\,n)=\dfrac{1}{a}+\dfrac{1}{a+d}+\cdots+\dfrac{1}{a+nd} \]
が整数にならないことでしたね^^補題3より,
\[ a+d,\quad a+2d,\quad\cdots\quad a+nd \]
のいずれかが $p^\alpha$ で割り切れるような素数 $p$ と正の整数 $\alpha$
で,$p^\alpha\gt n$ をみたすようなものが存在します.ここで,$\alpha$ は最大のものを選ぶと約束しておきます.すなわち,$p^{\alpha+1}$ で割り切れる項はない,としておきます.
$p^\alpha$ で切れるもので最小の項を $a+kd=p^\alpha x\,\,(1\leqq k\leqq n)$ とします.
ここで,$d$ が $p$ で割り切れるとすると,$a=p^\alpha x-kd$ より,$a$ も $p$ で割り切れることになり,$a$ と $d$ が互いに素であることに反します.よって,$d$ は $p$ で割り切れません.
また,$a$ が $p^\alpha$ で割り切れるとすると,$kd=p^\alpha x-a$ より,$kd$ も $p^\alpha$ で割り切れることになりますが,$d$ が $p$ で割り切れないことと,$1\leqq k\leqq n\lt p^\alpha$ より,それは不可能です.よって,$a$ は $p^\alpha$ で割り切れません.
$a+kd$ 以外に $p^\alpha$ で割り切れる項があったとして,それを $a+ld=p^\alpha y\,\,(k\lt l)$ とします.
\[ (a+ld)-(a+kd)=(l-k)d=p^{\alpha}(y-x) \]
と $d$ が $p$ で割り切れないことから,$l-k$ が $p^\alpha$ で割り切れることになりますが,
\[ 0\lt l-k\lt n\lt p^\alpha \]
より,それは不可能です.すなわち,$p^\alpha$ で割り切れる項は $a+kd$ の1つしかありません.$a$,$a+d$,$\cdots$,$a+nd$ の最小公倍数を $L$ とします.$L$ は $p$ でちょうど $\alpha$ 回割り切れます.
\[ LS(a,\,d,\,n)=\dfrac{L}{a}+\dfrac{L}{a+d}+\cdots+\dfrac{L}{a+kd}+\cdots+\dfrac{L}{a+nd} \]
を考えます.もし,$S(a,\,d,\,n)$ が整数であったとすると,左辺は $p$ の倍数になります.一方右辺において,項はすべて整数であり,$\dfrac{L}{a+kd}$ 以外の項については,分子 $L$ は $p$ で $\alpha$ 回割り切れ,分母は $p$ で $\alpha-1$ 回以下しか割り切れないのですべて $p$ の倍数になります.
$\dfrac{L}{a+kd}$ のみ,分子・分母がともに $p$ でちょうど $\alpha$ 回割り切れるので $p$ の倍数になりません.
すなわち,左辺は $p$ の倍数だけど,右辺は $p$ の倍数ではありません.矛盾です!
以上により,$d\geqq 4$ のとき,$S(a,\,d,\,n)$ は整数にならないことが示されました.
これで,定理3の証明は完成です!!
お疲れ様でした~^^
おわりに
この記事の冒頭で定義した第 $n$ 調和数 $H_n$ ですが,$2^m\leqq n\lt 2^{m+1}$ とすると,
\begin{align*}
H_n&=1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+\dfrac{1}{8}+\dfrac{1}{9}+\cdots+\dfrac{1}{2^m}+\cdots+\dfrac{1}{n}\\
&\geqq 1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+\dfrac{1}{8}+\dfrac{1}{9}+\cdots+\dfrac{1}{2^m}\\
&\gt 1+\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{8}+\dfrac{1}{8}+\dfrac{1}{8}+\dfrac{1}{16}+\cdots\cdots+\dfrac{1}{2^m}\\
&=1+\dfrac{1}{2}+\dfrac{1}{2}+\dfrac{1}{2}+\cdots\cdots+\dfrac{1}{2}=1+\dfrac{m}{2}
\end{align*}
なので,$n$ の値を大きくしていくと,$H_n$ の値はいくらでも大きくなることが分かります.いくらでも大きくなるのに,無数に存在する整数の値をすべて避けながら大きくなっていくというのは,なんとも不思議ですね^^!
この記事で解説した定理3の証明は,参考文献[3]の証明が元になっています.
ただし証明をいくつかの補題に分割し,証明の順序や一部の記号を変更しました.
最初,「そこまで難しくないだろう」と軽い気持ちで定理3の証明を調べ始めたのですが,文献[3]の証明は想像以上に技巧的で,著者のエルデシュの天才ぶりに感動しっぱなしでした^^!
この記事を通して数学に興味をもってくれる方が増えるのはもちろん嬉しいことですが,「長年定理3の証明を知りたかったけど,この記事を読んで初めて知ることができた」という方が現れてくれたら,最高に嬉しいです!!
参考文献
[1] Theisinger, L., "Bemerkung über die harmonische Reihe", Monatshefte für Mathematik und Physik, vol. 26 (1915), pp. 132--134.
[2] Kürschák, J., "A harmonikus sorról", Mathematikai és Fizikai Lapok, vol. 27 (1918), pp. 299--300.
[3] Erdős, P., "Egy Kürschák-féle elemi számelméleti tétel általánosítása", Matematikai és Fizikai Lapok, vol. 39 (1932), pp. 17--24.
コメントを残す
