「数学・パズル」の記事一覧
(13 件中 1 ~ 10 件目)
2023年3月16日
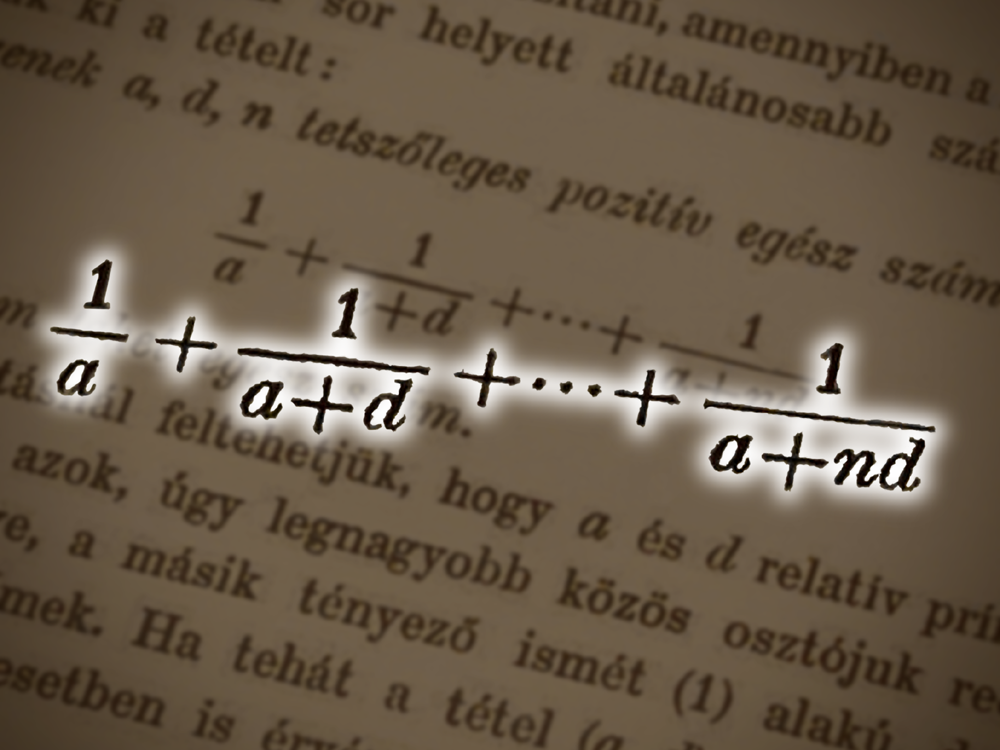
自然数 $n$ に対し,第 $n$ 調和数(harmonic number)$H_n$ を
$n\geqq 2$のとき,$H_n$の値は整数にならないことが知られています.
これは割と有名な結果で,高校生向けの受験参考書にも証明問題が掲載されているのを見たことがあります($n$ が素数の場合が出題されていたと記憶しています).
この結果にはいろいろな拡張が知られていますが,それらの一部をまとめると次のようになります:
きれいに段階的な拡張になっていますね!
この記事では,定理3の証明を最終目標に,途中で定理2の証明もご紹介します.
\[ H_n=1+\dfrac{1}{2}+\dfrac{1}{3}+\cdots+\dfrac{1}{n} \]
と定義します.$n\geqq 2$のとき,$H_n$の値は整数にならないことが知られています.
これは割と有名な結果で,高校生向けの受験参考書にも証明問題が掲載されているのを見たことがあります($n$ が素数の場合が出題されていたと記憶しています).
この結果にはいろいろな拡張が知られていますが,それらの一部をまとめると次のようになります:
定理1(タイシンガー,1915年)
$n$ を $2$ 以上の整数とするとき,
\[ 1+\dfrac12+\dfrac13+\dots+\dfrac1n \]
は整数にならない.
定理2(クルシャーク,1918年)
$a$,$n$ を正の整数とするとき,
\[ \dfrac{1}{a}+\dfrac{1}{a+1}+\dots+\dfrac{1}{a+n} \]
は整数にならない.
定理3(エルデシュ,1932年)
$a$,$d$,$n$ を正の整数とするとき,
\[ \dfrac{1}{a}+\dfrac{1}{a+d}+\cdots+\dfrac{1}{a+nd} \]
は整数にならない.
この記事では,定理3の証明を最終目標に,途中で定理2の証明もご紹介します.
2022年1月16日

当塾では,毎年生徒さん宛ての年賀状に数学のパズルや問題を載せていて,解けた生徒さんにはささやかながらお年玉を差し上げています^^
出題するのは,オリジナルのパズルだったり,その年に私が解いた問題で面白かったものをアレンジした問題などです。
今年は次の問題を出題しました:
例えば,$1234$ の場合
(1) $91\to 91+9+1=101$,$100\to 100+1=101$ のように「計算」の結果が同じ値になる2つの自然数の組があります。このような2つの自然数の組を他にも見つけましょう。
(2) 「計算」の結果が同じ値になる3つの自然数の組を見つけましょう。
(3) (2) の「3つ」の部分を4つ,5つ,…とどれだけ大きな数にしても,そのような自然数の組を見つけることができることを証明しなさい。
この問題は、2021年に私が解いた次の問題が元になっています:
出題するのは,オリジナルのパズルだったり,その年に私が解いた問題で面白かったものをアレンジした問題などです。
今年は次の問題を出題しました:
問題1
自然数に対し,その数にその数の各桁に現れる数をすべて加えるという「計算」をすることを考えます。例えば,$1234$ の場合
\begin{align*}
1234\,\,\to\,\, 1234+1+2+3+4=1244
\end{align*}
なので「計算」の結果は $1244$ です。(1) $91\to 91+9+1=101$,$100\to 100+1=101$ のように「計算」の結果が同じ値になる2つの自然数の組があります。このような2つの自然数の組を他にも見つけましょう。
(2) 「計算」の結果が同じ値になる3つの自然数の組を見つけましょう。
(3) (2) の「3つ」の部分を4つ,5つ,…とどれだけ大きな数にしても,そのような自然数の組を見つけることができることを証明しなさい。
2021年12月31日

こちらの記事では、漫画『数学ゴールデン』の第2巻第6話に登場する、多項式の問題の解説をします。
それは次の問題です:
このとき $a_2+a_4+a_6+a_8$ の値を求めよ.
作中では、この問題への異なる3種類の解法が登場します。
それぞれ、「がむしゃら展開」「定石」「最速アプローチ」として紹介されています。
最初「がむしゃら展開」を試みる主人公・小野田春一が、途中で先入観を捨て「最速アプローチ」に切り替えていく様が、成長シーンとして描かれています^^
それぞれのアプローチに対する詳細な計算は作中には描かれていません。
そこで、解法の名称と扱われ方から、私なりに解法の細部を予想してそれを補ったものをご紹介したいと思います。
それは次の問題です:
問題
多項式 $(x+1)^3(x+2)^3(x+3)^3$ における $x^k$ の係数を $a_k$ とおく.このとき $a_2+a_4+a_6+a_8$ の値を求めよ.
それぞれ、「がむしゃら展開」「定石」「最速アプローチ」として紹介されています。
最初「がむしゃら展開」を試みる主人公・小野田春一が、途中で先入観を捨て「最速アプローチ」に切り替えていく様が、成長シーンとして描かれています^^
それぞれのアプローチに対する詳細な計算は作中には描かれていません。
そこで、解法の名称と扱われ方から、私なりに解法の細部を予想してそれを補ったものをご紹介したいと思います。
2021年11月4日

数学業界(?)で「マスターデーモン」と呼ばれている整数の超難問があります。
次の問題です:
先日,Twitterでこの問題と再会しました。
「再会」と言ったのは,この問題はいろいろな数学の本で取り上げられている有名な問題で,解いたことはないものの存在は知っていたからです。
でもマスターデーモンと呼ばれていることは知りませんでした(正確には,かつて読んだことがあるけど忘れていました^^;)。
この記事では,この超難問を解説します。
できるだけ少ない予備知識で理解できるように,よく知られた整数論の結果なども証明を補いながら,高校数学の知識があれば分かるような解説を試みます。
また,この難問がマスターデーモンというインパクトのある名前で呼ばれるようになったいきさつについて私が調べたことや,調べていくうちに出会った整数論の公式についてもご紹介します。
次の問題です:
問題
$\dfrac{2^n+1}{n^2}$ が整数となるような $1$ より大きい整数 $n$ をすべて決定せよ。
「再会」と言ったのは,この問題はいろいろな数学の本で取り上げられている有名な問題で,解いたことはないものの存在は知っていたからです。
でもマスターデーモンと呼ばれていることは知りませんでした(正確には,かつて読んだことがあるけど忘れていました^^;)。
この記事では,この超難問を解説します。
できるだけ少ない予備知識で理解できるように,よく知られた整数論の結果なども証明を補いながら,高校数学の知識があれば分かるような解説を試みます。
また,この難問がマスターデーモンというインパクトのある名前で呼ばれるようになったいきさつについて私が調べたことや,調べていくうちに出会った整数論の公式についてもご紹介します。
2021年4月8日

待望の『数学ゴールデン』第2巻がついに発売しました!
私は楽天ブックスで注文していたのですが、到着したのは発売日の翌日でした^^;
到着後はもちろん即・読破しました!!
今回もたくさんの興味深い数学の問題が登場するのはもちろんですが、それ以外にも、数学がバリバリできる新キャラが登場したり、ちょっと恋愛要素(?)が加わったりと見どころ満載です^^♪
また、テストのシーンや、主人公・春一が(数学的に)進化するシーンは、まるでバトル漫画のような描写で表現されていて、第1巻以上に難問に立ち向かう少年たちのエネルギーを感じることができます!!
まさに数学というのは「紙の上の格闘技」ですね^^!!
今回の記事では、第2巻第5話に登場する「筧十三スペシャル宿題」にトライしてみました:
足す順番のみが異なる表し方は1通りと数える。
ただし、原題にはミスプリントと思われる部分があったのでそこだけ修正しました。
私は楽天ブックスで注文していたのですが、到着したのは発売日の翌日でした^^;
到着後はもちろん即・読破しました!!
今回もたくさんの興味深い数学の問題が登場するのはもちろんですが、それ以外にも、数学がバリバリできる新キャラが登場したり、ちょっと恋愛要素(?)が加わったりと見どころ満載です^^♪
また、テストのシーンや、主人公・春一が(数学的に)進化するシーンは、まるでバトル漫画のような描写で表現されていて、第1巻以上に難問に立ち向かう少年たちのエネルギーを感じることができます!!
まさに数学というのは「紙の上の格闘技」ですね^^!!
今回の記事では、第2巻第5話に登場する「筧十三スペシャル宿題」にトライしてみました:
問題
自然数 $n$ を $1$,$3$,$7$,$15$,$31$,$\cdots$($2$ の累乗 $-1$)の和で表す方法の数と,どの2つの数も $2$ 倍以上離れた数の和で表す方法の数は等しいことを示せ.足す順番のみが異なる表し方は1通りと数える。
2021年2月18日

今、数学漫画業界(?)で一番アツい漫画!
それが『数学ゴールデン』ですっ!!
待望の第2巻が2月26日(金)についに発売ですネ!!
…私はもちろん楽天ブックスで予約済みですっ!!^^
この作品の魅力の1つは、作中にリアルな、数学オリンピックレベルの問題が登場して、主人公たちとともに難問に挑戦することができることです!
今回の記事では、第1巻第4話に登場した次の「方程式」の問題にトライしてみました:
主人公の少年が、ともに数学を学ぶ仲間たちに徐々に心を開いていく、重要なシーンに登場する問題です。
それが『数学ゴールデン』ですっ!!
待望の第2巻が2月26日(金)についに発売ですネ!!
…私はもちろん楽天ブックスで予約済みですっ!!^^
この作品の魅力の1つは、作中にリアルな、数学オリンピックレベルの問題が登場して、主人公たちとともに難問に挑戦することができることです!
今回の記事では、第1巻第4話に登場した次の「方程式」の問題にトライしてみました:
問題
次の等式を満たす正の実数 $x$ を求めよ。
\[ x+\textstyle\sqrt{x(x+1)}+\sqrt{x(x+2)}+\sqrt{(x+1)(x+2)}=2 \]
2021年1月14日

私・大島が今一番注目している漫画『数学ゴールデン』!数学オリンピック日本代表を目指す少年たちの熱い青春の物語ですっ!!
この作品の魅力の1つは、ストーリーの中で主人公たちが取り組む数学の問題が実際に掲載されていて、主人公たちと一緒に悩むことができることです^^
この記事では、第1巻第2話に登場した「不定方程式」の問題を一緒に考えてみようと思います:
この問題に関して、私なりのアプローチと解説をお届けしたいと思います。
この作品の魅力の1つは、ストーリーの中で主人公たちが取り組む数学の問題が実際に掲載されていて、主人公たちと一緒に悩むことができることです^^
この記事では、第1巻第2話に登場した「不定方程式」の問題を一緒に考えてみようと思います:
問題
$2^a+3^b+1=6^c$ を満たす自然数 $(a,b,c)$ の組をすべて求めよ
2020年12月24日

先日、twitterを眺めていたら面白いマンガに出会いました。
『数学ゴールデン』です!!: 第一話が試し読みできたのですが、面白すぎて、読み終わった後、即楽天ブックスで第1巻を購入しました^^
第一話が試し読みできたのですが、面白すぎて、読み終わった後、即楽天ブックスで第1巻を購入しました^^
数学オリンピックに青春をかける高校生たちの物語ですっ!
『数学ゴールデン』です!!:

数学オリンピックに青春をかける高校生たちの物語ですっ!
2020年12月1日
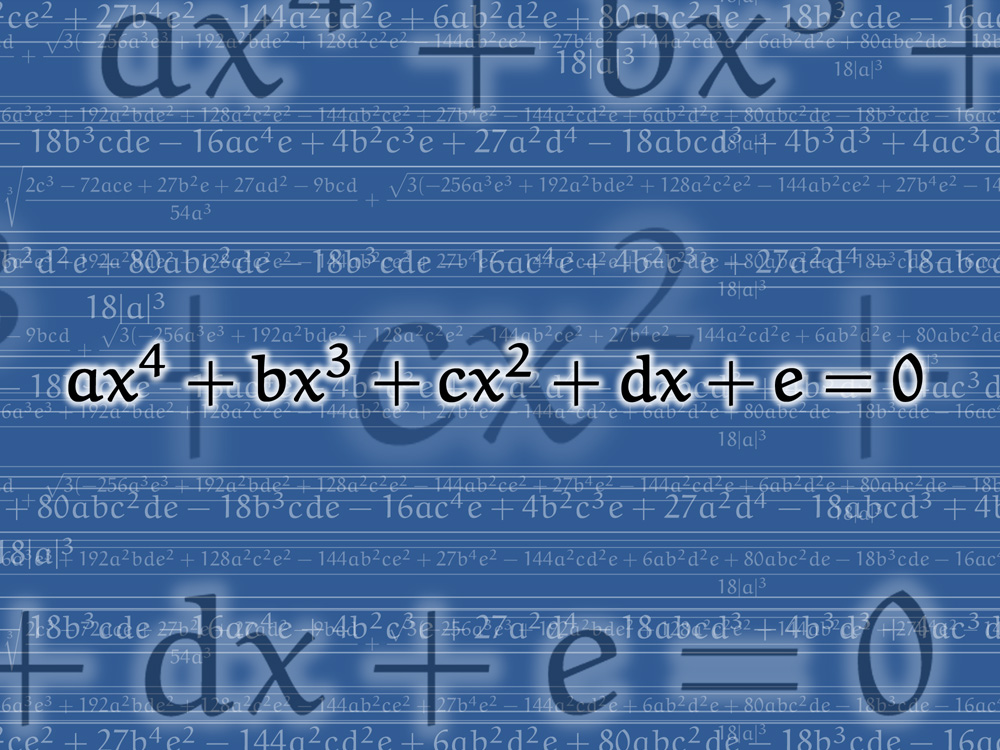
以前,3次方程式の解の公式について書きました:
3次方程式の解の公式 ~ カルダノの公式 »
その記事の中で,カルダノの弟子のフェラーリが4次方程式の解の公式を発見したことについて触れました。
今回の記事では,そのフェラーリが発見した4次方程式の解の公式をご紹介しようと思います!!
3次方程式の解の公式 ~ カルダノの公式 »
その記事の中で,カルダノの弟子のフェラーリが4次方程式の解の公式を発見したことについて触れました。
今回の記事では,そのフェラーリが発見した4次方程式の解の公式をご紹介しようと思います!!
2020年11月10日2020年11月13日
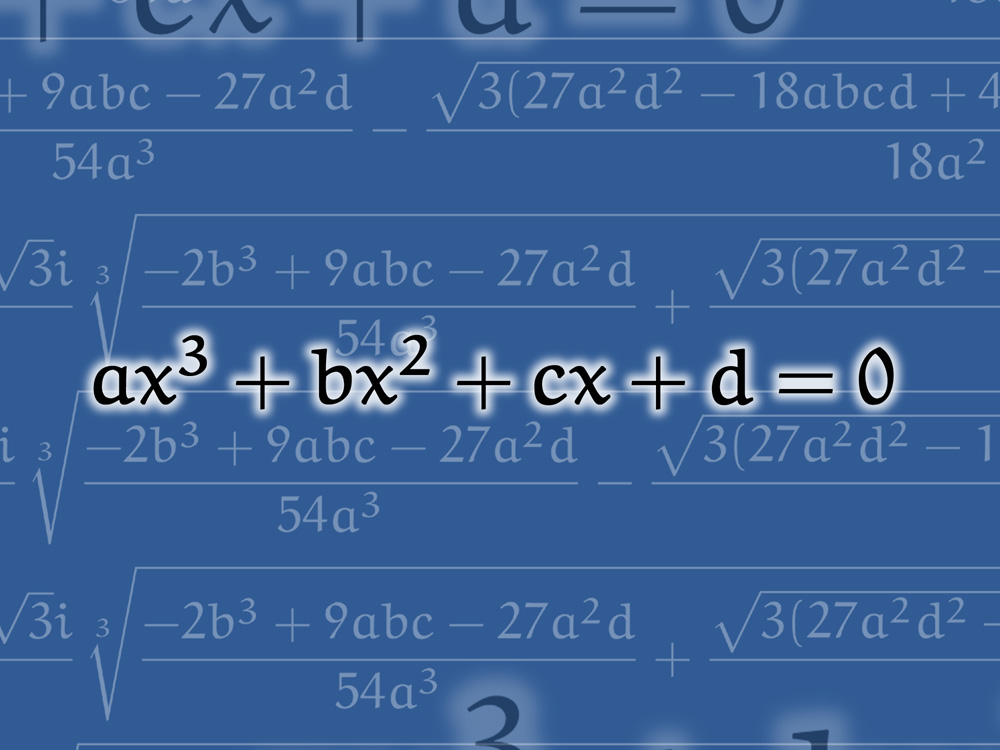
2次方程式の解の公式は,高校入試までには確実に習得しておかなければならない重要な公式です:
$ax^2+bx+c=0\,(a\neq 0)$の解は,
$$ \displaystyle x=\frac{-b\pm\sqrt{b^2-4ac}}{2a} $$
一方で,3次以上の高次方程式については,中学や高校で解の公式(またはそれに類する一般的な解法)を学習することはありません。$$ \displaystyle x=\frac{-b\pm\sqrt{b^2-4ac}}{2a} $$
(13 件中 1 ~ 10 件目)
