3次方程式の解の公式 ~ カルダノの公式
2020年11月10日
2020年11月13日
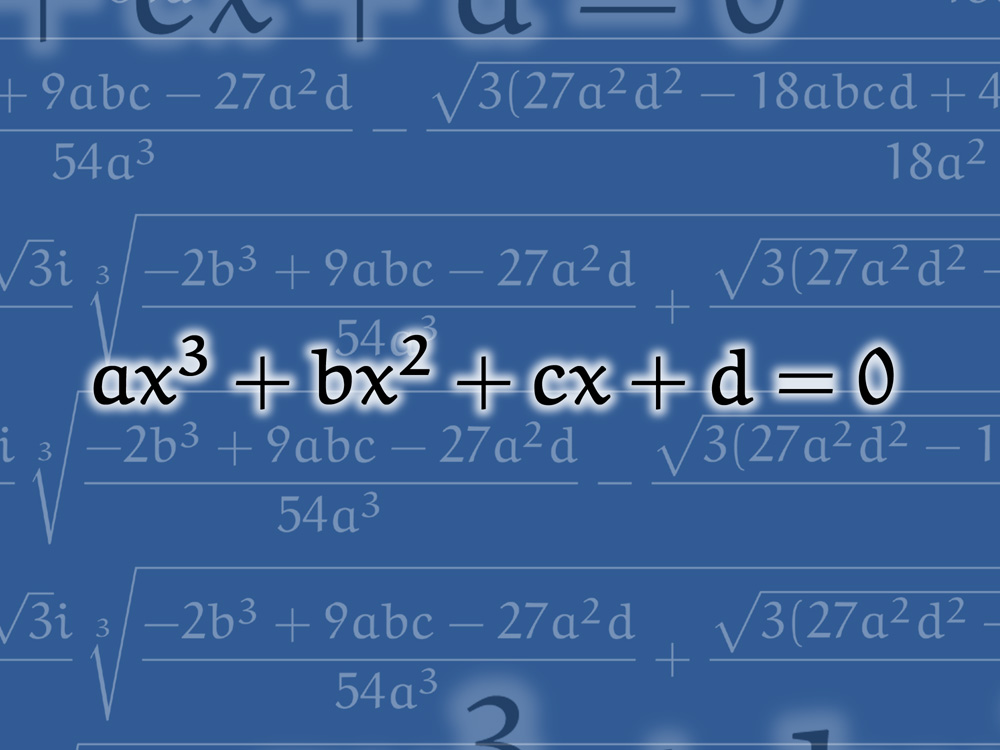
2次方程式の解の公式は,高校入試までには確実に習得しておかなければならない重要な公式です:
$ax^2+bx+c=0\,(a\neq 0)$の解は,
$$ \displaystyle x=\frac{-b\pm\sqrt{b^2-4ac}}{2a} $$
一方で,3次以上の高次方程式については,中学や高校で解の公式(またはそれに類する一般的な解法)を学習することはありません。$$ \displaystyle x=\frac{-b\pm\sqrt{b^2-4ac}}{2a} $$
高校数学・大学入試で求められるのは,まず解の1つ目を自力で見つけて,因数定理や組立除法を使って因数分解し,残りの解を求めていくという解法です。
一例として,3次方程式 $x^3=1$ を解いてみましょう。
1つ目の解として,$x=1$ はすぐに見つかります。
因数定理によると,3次式 $x^3-1$ は $x-1$ を因数にもちます。実際,
この分解により得られた2次方程式 \[ x^2+x+1=0 \] を解の公式を使って解くと, \[ x=\frac{-1\pm\sqrt{3}\,i}{2} \] が得られます。これで,$x=1$ とあわせて,3次方程式 $x^3=1$ の3つの解が求まりました。
でも,学問的な探求という意味で3次方程式の解の公式の証明を知っておくことは無駄にはならないでしょう。
この記事では,「カルダノの公式」とも呼ばれている,最もポピュラーな3次方程式の解の公式をご紹介します。
2次方程式の解の公式は大昔から知られていたようです。それに対して,3次方程式になるとグッと難しくなり,解の公式の発見は16世紀まで待たなければなりませんでした。
3次方程式の解の公式を最初に発見したのはデル・フェッロという人です。でも当時は「負の数」の概念が浸透しておらず,彼が発見したのは, \[ x^3+ax=b \] という形の方程式の解法でした。
当時は,数学者がお互いに難問を出題しあい,どっちがたくさん問題を解けたかを競う数学バトルが流行っていたので,数学者が優れた解法を発見しても,それを自分の心の中にそっとしまっておくのが普通だったみたいです。
フェッロも解法を公にすることはなく,弟子のフィオーレがその解法を引き継ぎました。
次に3次方程式の解法に進展をもたらしたのはタルターリャです。彼は1535年に, \[ x^3+ax^2=b \] の形の方程式の解法を発見したことを公表します。
それを聞いてやってきたフィオーレとの数学試合にも見事勝利しますが,やはり数学者の秘密主義のため解法を公にはしませんでした。
次に登場するのが「カルダノの公式」にも名を残すカルダノです!
カルダノはタルターリャに「解の公式教えてっ!お願いっ!!」と言います。最初は「ダメだよ」って言っていたタルターリャも,しつこく「お願いっ!!」と言われているうちに,「じゃあ…2人だけの秘密だよ」と最後は教えてしまいます。このことが後に両者の間で論争となります^^;
カルダノがタルターリャから3次方程式の解の公式を教えてもらった後,カルダノの弟子のフェラーリという人物が,4次方程式の解の公式を発見します。
1545年,カルダノが『アルス・マグナ』(ラテン語で"偉大な方法")という本を出版します。その本には,タルターリャに教えてもらった3次方程式の解法や,弟子のフェラーリが発見した4次方程式の解法が書いてあります。
タルターリャは「秘密って言ったじゃん!!」とブチ切れして,「数学試合だ!!」ってなるのですが,カルダノは弟子のフェラーリを試合に出し,両者の試合は引き分けに終わります。
…とここまでは数学愛好家の間では結構有名な話です。
ここだけ読むとカルダノは他の人の業績を盗んだヤツっていうイメージですが,実際には『アルス・マグナ』の中で,「フェッロとタルターリャが3次方程式の解法を見つけたんだぞ!2人はスゲーんだぞ!!」ってちゃんと書いてあるみたいですし,いろいろな形の3次方程式の解法をまとめて表した業績などもあるみたいです^^
4次方程式の解の公式が発見されたとなると,次はもちろん5次方程式となるわけですが,残念ながら5次方程式の解の公式は存在しません。発見されていないのではありません。「我々が期待するような解の公式は存在しないことが証明された」のです!!
数学の問題を考えるときには,何をもって「解けた」こととするのかという条件を明確にするのが重要です。
我々が「解の公式」に求めているのは,方程式の係数から出発して,四則演算とべき根をとる操作の有限回の繰り返しで,方程式の解を得ることができる計算の方法・手順を知ることです。
例えば3次方程式に関しても,円錐曲線を用いて方程式の解を幾何的に表す方法は古代ギリシアの時代に始まり,11世紀ごろには既に知られていました。
また5次方程式に対しても,楕円積分などの超越的手法を用いることで解を表示することはできます。
でもこれらは我々が求めている解の公式ではありません!!
5次方程式には(我々の求める,係数から四則演算とべき根だけで解を表示するタイプの)解の公式は存在しないことは,1824年にアーベルによって証明されました。ルフィニという人の貢献も大きかったらしく,現在この事実は「アーベル-ルフィニの定理」と呼ばれています。
5次方程式に解の公式が存在しなかったことを受けて,どのようなときに解の公式が存在するのか?ということが研究の対象となり,それらは「ガロア理論」という壮大な理論につながっていきます。
まずは,方程式を簡単にしていきます。
$x^3$ の係数を $1$ にするために,両辺を $a\,(\neq 0)$ で割って,
この方程式の解を $p$,$q$ の式で表すことができれば,$a$,$b$,$c$,$d$ で表すこともでき,$x=y-\frac{b}{3a}$ なので,解 $x$ を係数で表すことができ,我々の求める解の公式が得られたことになります。
以下,方程式 $(2)$ について考えていきます。
突然ですが,方程式 $(2)$ において $y=u+v$ と変換します。
ここで,この方程式から,
$(4)$ を満たす $u$,$v$ が求めることができれば,それらは $(3)$ を満たします。すなわち,$y=u+v$ が $(2)$ を満たすので問題解決です^^♪
以下, $(4)$ を満たす $u$,$v$ を求めていくのですが,ここで「方程式の解を $(4)$ を満たすものに限定して考えていいの?」と疑問に思うかもしれません。
でも大丈夫なんです!「代数学の基本定理」というものがあって「(複素数係数の)3次方程式は(重解も含めて)3つの複素数解をもつ」ということは保証されているので,どんな形でも解が3つ得られればO.K.というワケです。
$(4)$ をちょっと変形すると,
$u^3$と$v^3$の和と積が与えられているので,2次方程式の解と係数の関係を考えると,$u^3$,$v^3$は,2次方程式
2次方程式の解の公式より,
以下,$u$,$v$ を決定していき,方程式 $(2)$ の解 $y$ を $p$,$q$ の式として表していきます。
一般に,複素数 $\alpha\in\mathbb{C}$ に対して,$\alpha$ の立方根,すなわち方程式
その3つの解の関係性を表すために,この記事の序盤の注で述べた $\omega$ を使います。
$(6)$ の解の1つを便宜的に $z=\sqrt[3]{\alpha}$ と書くことにします。このとき,
つまり,複素数 $\alpha$ に対して,$\alpha$ の立方根は3つあり,その1つを $\sqrt[3]{\alpha}$ と書くと,残り2つは $\sqrt[3]{\alpha}\,\omega$,$\sqrt[3]{\alpha}\,\omega^2$ となることが分かります。
それでは,以上のことをふまえて $(5)$ から $u$,$v$ を決定していきます。
次に,$v$ についても同様に立方根を考えていくのですが,1つ注意点があります。
我々はそもそも $(4)$ の方程式を考えていたので,
$z=-p$ は明らかに解なので,$u_1 v_k\,(k=1,\,2,\,3)$ のどれかは $-p$ と一致します。
その一致した $v_k$ をあらためて
これにより,$(u_1,\,v_1)$,$(u_2,\,v_2)$,$(u_3,\,v_3)$ という $(4)$ の3組の解を見つけることができました!
この3組の解を用いて,方程式 $(2)$ の解は,
方程式 $(2)$ は,$x=y-\frac{b}{3a}$ という式で元の方程式 $(1)$ と結ばれていました。
よって方程式 $(1)$ の解は,
$p$,$q$ は,
…と言っても,$p$,$q$ の式を代入してひたすら計算するだけです^^;
$\omega$,$\omega^2$ の値も補って,解の公式を完全な(?)形で書いておきます:
私はこんな複雑な数式を見るとワクワクします(笑)
皆さんはどうですか?^^
最後には,非常に複雑な式が登場しましたが,もちろんこれを記憶する必要はありません。
証明の途中に現れる式変形のアイディアは,自分で問題を考えるときにも役立つかもしれません。
高校生ぐらいだと証明自体を理解することも,方程式のよい学習になると思います。
是非,解の公式に発見に関わった数学者達に思いをはせながら,証明を味わってみてください。
一例として,3次方程式 $x^3=1$ を解いてみましょう。
1つ目の解として,$x=1$ はすぐに見つかります。
因数定理によると,3次式 $x^3-1$ は $x-1$ を因数にもちます。実際,
\[ x^3-1=(x-1)(x^2+x+1) \]
と因数分解されます(この式は因数分解の基本公式でもあります)。この分解により得られた2次方程式 \[ x^2+x+1=0 \] を解の公式を使って解くと, \[ x=\frac{-1\pm\sqrt{3}\,i}{2} \] が得られます。これで,$x=1$ とあわせて,3次方程式 $x^3=1$ の3つの解が求まりました。
注)ここで,後の計算のために記号を定義しておきます。
\[ \omega=\frac{-1+\sqrt{3}\,i}{2} \]
とおくと,簡単な計算により,
\[ \omega^2=\frac{-1-\sqrt{3}\,i}{2} \]
となることが分かり,3次方程式 $x^3=1$ の3つの解は,$x=1$,$\omega$,$\omega^2$ と簡潔に表されます。もちろん,$\omega^3=1$,$(\omega^2)^3=1$ となります。
3次方程式の解の公式は,入試等で必要というワケではなく,上で述べたのと同様の解法を使いこなすことができれば困ることはありません。でも,学問的な探求という意味で3次方程式の解の公式の証明を知っておくことは無駄にはならないでしょう。
この記事では,「カルダノの公式」とも呼ばれている,最もポピュラーな3次方程式の解の公式をご紹介します。
発見の歴史など
証明に入る前に,代数方程式の解の公式の歴史について簡単に触れておこうと思います。2次方程式の解の公式は大昔から知られていたようです。それに対して,3次方程式になるとグッと難しくなり,解の公式の発見は16世紀まで待たなければなりませんでした。
3次方程式の解の公式を最初に発見したのはデル・フェッロという人です。でも当時は「負の数」の概念が浸透しておらず,彼が発見したのは, \[ x^3+ax=b \] という形の方程式の解法でした。
当時は,数学者がお互いに難問を出題しあい,どっちがたくさん問題を解けたかを競う数学バトルが流行っていたので,数学者が優れた解法を発見しても,それを自分の心の中にそっとしまっておくのが普通だったみたいです。
フェッロも解法を公にすることはなく,弟子のフィオーレがその解法を引き継ぎました。
次に3次方程式の解法に進展をもたらしたのはタルターリャです。彼は1535年に, \[ x^3+ax^2=b \] の形の方程式の解法を発見したことを公表します。
それを聞いてやってきたフィオーレとの数学試合にも見事勝利しますが,やはり数学者の秘密主義のため解法を公にはしませんでした。
次に登場するのが「カルダノの公式」にも名を残すカルダノです!
カルダノはタルターリャに「解の公式教えてっ!お願いっ!!」と言います。最初は「ダメだよ」って言っていたタルターリャも,しつこく「お願いっ!!」と言われているうちに,「じゃあ…2人だけの秘密だよ」と最後は教えてしまいます。このことが後に両者の間で論争となります^^;
カルダノがタルターリャから3次方程式の解の公式を教えてもらった後,カルダノの弟子のフェラーリという人物が,4次方程式の解の公式を発見します。
1545年,カルダノが『アルス・マグナ』(ラテン語で"偉大な方法")という本を出版します。その本には,タルターリャに教えてもらった3次方程式の解法や,弟子のフェラーリが発見した4次方程式の解法が書いてあります。
タルターリャは「秘密って言ったじゃん!!」とブチ切れして,「数学試合だ!!」ってなるのですが,カルダノは弟子のフェラーリを試合に出し,両者の試合は引き分けに終わります。
…とここまでは数学愛好家の間では結構有名な話です。
ここだけ読むとカルダノは他の人の業績を盗んだヤツっていうイメージですが,実際には『アルス・マグナ』の中で,「フェッロとタルターリャが3次方程式の解法を見つけたんだぞ!2人はスゲーんだぞ!!」ってちゃんと書いてあるみたいですし,いろいろな形の3次方程式の解法をまとめて表した業績などもあるみたいです^^
4次方程式の解の公式が発見されたとなると,次はもちろん5次方程式となるわけですが,残念ながら5次方程式の解の公式は存在しません。発見されていないのではありません。「我々が期待するような解の公式は存在しないことが証明された」のです!!
数学の問題を考えるときには,何をもって「解けた」こととするのかという条件を明確にするのが重要です。
我々が「解の公式」に求めているのは,方程式の係数から出発して,四則演算とべき根をとる操作の有限回の繰り返しで,方程式の解を得ることができる計算の方法・手順を知ることです。
例えば3次方程式に関しても,円錐曲線を用いて方程式の解を幾何的に表す方法は古代ギリシアの時代に始まり,11世紀ごろには既に知られていました。
また5次方程式に対しても,楕円積分などの超越的手法を用いることで解を表示することはできます。
でもこれらは我々が求めている解の公式ではありません!!
5次方程式には(我々の求める,係数から四則演算とべき根だけで解を表示するタイプの)解の公式は存在しないことは,1824年にアーベルによって証明されました。ルフィニという人の貢献も大きかったらしく,現在この事実は「アーベル-ルフィニの定理」と呼ばれています。
5次方程式に解の公式が存在しなかったことを受けて,どのようなときに解の公式が存在するのか?ということが研究の対象となり,それらは「ガロア理論」という壮大な理論につながっていきます。
- 以上,数学史に関する部分は『岩波数学入門辞典』とWikipediaを参考にしました。数学者の名前のカタカナ表記は数学入門辞典にあわせました。
方程式を簡単にする
それでは,3次方程式の解の公式の計算を始めましょう!
\[ ax^3+bx^2+cx+d=0\,\,(a\neq 0)\quad\cdots\,(1) \]
という3次方程式を解くことを考えます。$a$,$b$,$c$,$d$ はすべて複素数とします。まずは,方程式を簡単にしていきます。
$x^3$ の係数を $1$ にするために,両辺を $a\,(\neq 0)$ で割って,
\[ x^3+\frac{b}{a}x^2+\frac{c}{a}x+\frac{d}{a}=0 \]
次に,$x^2$ の項を消去するために $x=y-\frac{b}{3a}$ と変換します。これは2次方程式における平方完成にあたる変形で,このような変換を「チルンハウス変換」と呼ぶらしいです。
\begin{align*}
&x^3+\frac{b}{a}x^2+\frac{c}{a}x+\frac{d}{a}\\[5pt]
=\,&\bigg(y-\frac{b}{3a}\bigg)^3+\frac{b}{a}\bigg(y-\frac{b}{3a}\bigg)^2+\frac{c}{a}\bigg(y-\frac{b}{3a}\bigg)+\frac{d}{a}\\[5pt]
=\,&y^3-\frac{b}{a}y^2+\frac{b^2}{3a^2}y-\frac{b^3}{27a^3}+\frac{b}{a}y^2-\frac{2b^2}{3a^2}y+\frac{b^3}{9a^3}+\frac{c}{a}y-\frac{bc}{3a^2}+\frac{d}{a}\\[5pt]
=\,&y^3+\bigg(-\frac{b^2}{3a^2}+\frac{c}{a}\bigg)y+\frac{2b^3}{27a^3}-\frac{bc}{3a^2}+\frac{d}{a}\\
\end{align*}
なので,
\begin{align*}
3p&=-\frac{b^2}{3a^2}+\frac{c}{a},\\[5pt]
2q&=\frac{2b^3}{27a^3}-\frac{bc}{3a^2}+\frac{d}{a}
\end{align*}
と置きかえすると,元の方程式は,
\[ y^3+3py+2q=0\quad\cdots\,(2)\]
と表されます。係数の $3$ や $2$ は後で式が簡単になるので付けています。この方程式の解を $p$,$q$ の式で表すことができれば,$a$,$b$,$c$,$d$ で表すこともでき,$x=y-\frac{b}{3a}$ なので,解 $x$ を係数で表すことができ,我々の求める解の公式が得られたことになります。
以下,方程式 $(2)$ について考えていきます。
$y=u+v$ と変換
ここからが,この証明におけるもっとも技巧的な部分です。突然ですが,方程式 $(2)$ において $y=u+v$ と変換します。
\begin{align*}
&y^3+3py+2q\\
=\,&(u+v)^3+3p(u+v)+2q\\
=\,&u^3+3u^2v+3uv^2+v^3+3p(u+v)+2q\\
=\,&u^3+v^3+3uv(u+v)+3p(u+v)+2q\\
=\,&u^3+v^3+2q+3(u+v)(uv+p)
\end{align*}
なので,方程式 $(2)$ は,
\[ u^3+v^3+2q+3(u+v)(uv+p)=0\quad\cdots\,(3) \]
と書き換えられます。ここで,この方程式から,
\begin{align*}
\left\{\begin{array}{l}
u^3+v^3+2q=0\\
uv+p=0
\end{array}\right.\quad\cdots\,(4)
\end{align*}
という2つの方程式をつくります。$(4)$ を満たす $u$,$v$ が求めることができれば,それらは $(3)$ を満たします。すなわち,$y=u+v$ が $(2)$ を満たすので問題解決です^^♪
以下, $(4)$ を満たす $u$,$v$ を求めていくのですが,ここで「方程式の解を $(4)$ を満たすものに限定して考えていいの?」と疑問に思うかもしれません。
でも大丈夫なんです!「代数学の基本定理」というものがあって「(複素数係数の)3次方程式は(重解も含めて)3つの複素数解をもつ」ということは保証されているので,どんな形でも解が3つ得られればO.K.というワケです。
$(4)$ をちょっと変形すると,
\begin{align*}
\left\{\begin{array}{l}
u^3+v^3=-2q\\
u^3v^3=-p^3
\end{array}\right.
\end{align*}
という式が得られます。$u^3$と$v^3$の和と積が与えられているので,2次方程式の解と係数の関係を考えると,$u^3$,$v^3$は,2次方程式
\[ t^2+2qt-p^3=0 \]
の解になることが分かります。2次方程式の解の公式より,
\[ t=-q\pm\sqrt{q^2+p^3} \]
と2つの解が得られますが,$u^3$,$v^3$についての条件は対称なので,
\begin{align*}
\left\{\begin{array}{l}
u^3=-q+\sqrt{q^2+p^3}\\
v^3=-q-\sqrt{q^2+p^3}
\end{array}\right.\quad\cdots\,(5)
\end{align*}
と決めても大丈夫です。以下,$u$,$v$ を決定していき,方程式 $(2)$ の解 $y$ を $p$,$q$ の式として表していきます。
$p$,$q$ で表す
$(5)$ から立方根をとって $u$,$v$ を決定する際に注意点があります。一般に,複素数 $\alpha\in\mathbb{C}$ に対して,$\alpha$ の立方根,すなわち方程式
\[ z^3=\alpha\quad\cdots\,(6) \]
を満たす $z$ は,代数学の基本定理により3つあるはずです。その3つの解の関係性を表すために,この記事の序盤の注で述べた $\omega$ を使います。
$(6)$ の解の1つを便宜的に $z=\sqrt[3]{\alpha}$ と書くことにします。このとき,
\begin{align*}
&(\sqrt[3]{\alpha}\,\omega)^3=\alpha\,\omega^3=\alpha\\
&(\sqrt[3]{\alpha}\,\omega^2)^3=\alpha\,(\omega^2)^3=\alpha
\end{align*}
なので,$z=\sqrt[3]{\alpha}\,\omega$,$z=\sqrt[3]{\alpha}\,\omega^2$ も $(6)$ の解になります。つまり,複素数 $\alpha$ に対して,$\alpha$ の立方根は3つあり,その1つを $\sqrt[3]{\alpha}$ と書くと,残り2つは $\sqrt[3]{\alpha}\,\omega$,$\sqrt[3]{\alpha}\,\omega^2$ となることが分かります。
それでは,以上のことをふまえて $(5)$ から $u$,$v$ を決定していきます。
\[ u^3=-q+\sqrt{q^2+p^3}\quad\cdots\,(7) \]
より,右辺の立方根の1つを $\sqrt[3]{-q+\sqrt{q^2+p^3}}$ とすると,
\begin{align*}
u_1&=\sqrt[3]{-q+\sqrt{q^2+p^3}},\\
u_2&=\omega\,\sqrt[3]{-q+\sqrt{q^2+p^3}},\\
u_3&=\omega^2\,\sqrt[3]{-q+\sqrt{q^2+p^3}}
\end{align*}
が $(7)$ の3つの解になります。次に,$v$ についても同様に立方根を考えていくのですが,1つ注意点があります。
我々はそもそも $(4)$ の方程式を考えていたので,
\[ uv=-p \]
を満たすように $u$,$v$ を選ばなければなりません。
\[ v^3=-q-\sqrt{q^2+p^3}\quad\cdots\,(8) \]
を満たす $v$ のうち,上で最初に選んだ $u_1$ に対して,$u_1 v=-p$ を満たすものをとることを考えます。$(8)$ を満たす3つの $v$ を $v_1$,$v_2$,$v_3$ とすると,
\[ (u_1 v_k)^3=u_1{}^3v_k{}^3=-p^3\quad (k=1,\,2,\,3) \]
なので,$u_1 v_k\,(k=1,\,2,\,3)$ は方程式 $z^3=-p^3$ の3つの解です。$z=-p$ は明らかに解なので,$u_1 v_k\,(k=1,\,2,\,3)$ のどれかは $-p$ と一致します。
その一致した $v_k$ をあらためて
\[ v_1=\sqrt[3]{-q-\sqrt{q^2+p^3}} \]
と書くことにすると,
\begin{align*}
v_2&=\omega^2\,\sqrt[3]{-q-\sqrt{q^2+p^3}},\\
v_3&=\omega\,\sqrt[3]{-q-\sqrt{q^2+p^3}}
\end{align*}
はそれぞれ,$u_2 v_2=-p$,$u_3 v_3=-p$ を満たします。これにより,$(u_1,\,v_1)$,$(u_2,\,v_2)$,$(u_3,\,v_3)$ という $(4)$ の3組の解を見つけることができました!
この3組の解を用いて,方程式 $(2)$ の解は,
\begin{align*}
y_1&=u_1+v_1=\sqrt[3]{-q+\sqrt{q^2+p^3}}+\sqrt[3]{-q-\sqrt{q^2+p^3}},\\
y_2&=u_2+v_2=\omega\sqrt[3]{-q+\sqrt{q^2+p^3}}+\omega^2\sqrt[3]{-q-\sqrt{q^2+p^3}},\\
y_3&=u_3+v_3=\omega^2\sqrt[3]{-q+\sqrt{q^2+p^3}}+\omega\sqrt[3]{-q-\sqrt{q^2+p^3}}
\end{align*}
と表されます。方程式 $(2)$ は,$x=y-\frac{b}{3a}$ という式で元の方程式 $(1)$ と結ばれていました。
よって方程式 $(1)$ の解は,
\begin{align*}
x_1&=y_1-\frac{b}{3a}=-\frac{b}{3a}+\sqrt[3]{-q+\sqrt{q^2+p^3}}+\sqrt[3]{-q-\sqrt{q^2+p^3}},\\
x_2&=y_2-\frac{b}{3a}=-\frac{b}{3a}+\omega\sqrt[3]{-q+\sqrt{q^2+p^3}}+\omega^2\sqrt[3]{-q-\sqrt{q^2+p^3}},\\
x_3&=y_3-\frac{b}{3a}=-\frac{b}{3a}+\omega^2\sqrt[3]{-q+\sqrt{q^2+p^3}}+\omega\sqrt[3]{-q-\sqrt{q^2+p^3}}
\end{align*}
となります。$p$,$q$ は,
\begin{align*}
p&=\frac{-b^2+3ac}{9a^2},\\
q&=\frac{2b^3-9abc+27a^2d}{54a^3}
\end{align*}
と元の方程式 $(1)$ の係数で表すことができるので,これで我々の目標であった「解の公式」が得られたことになります。
$a$,$b$,$c$,$d$ で表す
最後に,「解の公式」を元の方程式 $(1)$ の係数 $a$,$b$,$c$,$d$ で表してみます。…と言っても,$p$,$q$ の式を代入してひたすら計算するだけです^^;
$\omega$,$\omega^2$ の値も補って,解の公式を完全な(?)形で書いておきます:
\begin{align}
x_1=&-\frac{b}{3a}+\sqrt[3]{\frac{-2b^3+9abc-27a^2d}{54a^3}+\frac{\sqrt{3(27a^2d^2-18abcd+4b^3d+4ac^3-b^2c^2)}}{18a^2}}\\
&+\sqrt[3]{\frac{-2b^3+9abc-27a^2d}{54a^3}-\frac{\sqrt{3(27a^2d^2-18abcd+4b^3d+4ac^3-b^2c^2)}}{18a^2}},\\
x_2=&-\frac{b}{3a}+\frac{-1+\sqrt{3}i}{2}\sqrt[3]{\frac{-2b^3+9abc-27a^2d}{54a^3}+\frac{\sqrt{3(27a^2d^2-18abcd+4b^3d+4ac^3-b^2c^2)}}{18a^2}}\\
&+\frac{-1-\sqrt{3}i}{2}\sqrt[3]{\frac{-2b^3+9abc-27a^2d}{54a^3}-\frac{\sqrt{3(27a^2d^2-18abcd+4b^3d+4ac^3-b^2c^2)}}{18a^2}},\\
x_3=&-\frac{b}{3a}+\frac{-1-\sqrt{3}i}{2}\sqrt[3]{\frac{-2b^3+9abc-27a^2d}{54a^3}+\frac{\sqrt{3(27a^2d^2-18abcd+4b^3d+4ac^3-b^2c^2)}}{18a^2}}\\
&+\frac{-1+\sqrt{3}i}{2}\sqrt[3]{\frac{-2b^3+9abc-27a^2d}{54a^3}-\frac{\sqrt{3(27a^2d^2-18abcd+4b^3d+4ac^3-b^2c^2)}}{18a^2}}
\end{align}
すごく長い式になりますね…^^;私はこんな複雑な数式を見るとワクワクします(笑)
皆さんはどうですか?^^
おわりに
以上,3次方程式の解の公式をご紹介しました。最後には,非常に複雑な式が登場しましたが,もちろんこれを記憶する必要はありません。
証明の途中に現れる式変形のアイディアは,自分で問題を考えるときにも役立つかもしれません。
高校生ぐらいだと証明自体を理解することも,方程式のよい学習になると思います。
是非,解の公式に発見に関わった数学者達に思いをはせながら,証明を味わってみてください。
コメントを残す
コメント一覧 (44)
こうたさん
2022-07-13 09:22:10
いいね!
大島学習塾さん
2022-07-31 07:46:12
こうた さん、コメントありがとうございます!^^
あさん
2022-10-11 19:56:22
すごい!
ゆうさん
2022-11-22 17:26:46
この一番下の公式って画像データでもらえますか?
大島学習塾さん
2022-11-22 18:58:11
あ さん、ありがとうございます。
本当にすごい公式ですよね!!
本当にすごい公式ですよね!!
大島学習塾さん
2022-11-22 19:10:00
ゆう さん、コメントありがとうございます。
このページ自体のソースコードにTeXのコードも含まれておりますので、再利用していただいても大丈夫です。
一応、インスタグラムにも貼っています:
https://www.instagram.com/p/CHFuSMIHCZy/
これらの方法で不足な場合は改めてコメントしてください。
このページ自体のソースコードにTeXのコードも含まれておりますので、再利用していただいても大丈夫です。
一応、インスタグラムにも貼っています:
https://www.instagram.com/p/CHFuSMIHCZy/
これらの方法で不足な場合は改めてコメントしてください。
ビリーさん
2022-12-20 10:04:35
すごい
チョコちゃんさん
2022-12-31 11:28:32
最後の解の公式のところでpやqが3乗されていないのは間違いでしょうか?
マスターベーションさん
2023-01-02 16:09:57
最後の解の部分でその前までpやqだったものが3乗されてない気がするのですがそれは気の所為でしょうか?もし間違えているんだったらちゃんと見直してから投稿するようにしていてください。
大島学習塾さん
2023-01-02 18:01:21
ビリーさん、コメントありがとうございます!
大島学習塾さん
2023-01-02 18:14:36
チョコちゃんさん、マスターベーションさん、コメントありがとうございます。
複数の方から同様の内容のご指摘をいただいたのですが、申し訳ないことに私が間違いを発見できません。
お手数ですが、もう少し具体的に間違いの箇所をご指摘いただけますと助かります。
一応、最後の式は正しいと思います。
元の方程式に代入するなどしてお確かめください。
投稿内容には細心の注意を払っておりますが、
入力ミスなどが存在するかもしれません。
今後も間違い箇所があればご指摘いただきますと幸いです。
よろしくお願いいたします。
複数の方から同様の内容のご指摘をいただいたのですが、申し訳ないことに私が間違いを発見できません。
お手数ですが、もう少し具体的に間違いの箇所をご指摘いただけますと助かります。
一応、最後の式は正しいと思います。
元の方程式に代入するなどしてお確かめください。
投稿内容には細心の注意を払っておりますが、
入力ミスなどが存在するかもしれません。
今後も間違い箇所があればご指摘いただきますと幸いです。
よろしくお願いいたします。
aspalaさん
2023-03-20 20:30:32
代数ソルバーで計算した所、解の完全な公式の√q^3+p^2を代入したところでの分母が18a^2ではなく、108a^4で、また、ルート内を3で括る必要がないようです。計算で自身がなくて代数ソルバーに計算させましたが、様々なところで計算させて同じ結果が出たので多分あっていると思います。確認をお願いします。
aspalaさん
2023-03-20 20:47:38
先程のことはすみませんでした。
もう何度も確認した所、全部あっていたようです。
約分があったので、それで間違ってしまっていたようです。
他にも探してみましたが、間違いが見つからなかったため多分あっているとは思います。
本当に申し訳ございませんでした
もう何度も確認した所、全部あっていたようです。
約分があったので、それで間違ってしまっていたようです。
他にも探してみましたが、間違いが見つからなかったため多分あっているとは思います。
本当に申し訳ございませんでした
大島学習塾さん
2023-03-22 08:35:46
aspala さん、コメントありがとうございます。
他のツールまで使って検証していただきありがとうございます。
私としても、誤った情報を発信するのは本意ではありませんので、計算ミスや誤字脱字などの些細なものも含め、正しくない情報があればコメントしていただけますととても助かります。
今後とも、当ブログをよろしくお願いいたします。
他のツールまで使って検証していただきありがとうございます。
私としても、誤った情報を発信するのは本意ではありませんので、計算ミスや誤字脱字などの些細なものも含め、正しくない情報があればコメントしていただけますととても助かります。
今後とも、当ブログをよろしくお願いいたします。
山下小百合さん
2023-04-13 05:28:01
すごい!次はこの解の公式を使って三次方程式の解を導き出してほしいです
大島学習塾さん
2023-04-14 16:17:24
山下小百合さん、コメントありがとうございます。
3次方程式の解の公式はご覧の通り非常に複雑で、具体的な方程式の解を求めるのは骨が折れます^^;
以前、3次方程式の解の公式を用いて、2次方程式の解の公式を求める計算をツイートしたことがございます。
是非ご覧ください^^:
https://twitter.com/oshima_juku/status/1519351042986889217
3次方程式の解の公式はご覧の通り非常に複雑で、具体的な方程式の解を求めるのは骨が折れます^^;
以前、3次方程式の解の公式を用いて、2次方程式の解の公式を求める計算をツイートしたことがございます。
是非ご覧ください^^:
https://twitter.com/oshima_juku/status/1519351042986889217
3次方程式の解を求めてみた!さん
2023-04-19 23:28:02
2023/1/1の頃
当然3次方程式の解が気になったので
3次方程式の解を求めてみました。
求めた解が同じかどうかを
確認してみました。
式変形してみると同じ解になったので
求めた式も解であることが
わかりました。
やっぱり求めた解はおもしろい!
当然3次方程式の解が気になったので
3次方程式の解を求めてみました。
求めた解が同じかどうかを
確認してみました。
式変形してみると同じ解になったので
求めた式も解であることが
わかりました。
やっぱり求めた解はおもしろい!
大島学習塾さん
2023-04-22 23:32:49
3次方程式の解を求めてみた!さん、コメントありがとうございます。
当ブログの記事がお役に立ったようで、よかったです。
当ブログの記事がお役に立ったようで、よかったです。
はむきちさん
2023-06-18 12:05:49
ちょうど3次方程式の解の公式を暗記したかったので細かい説明まで載っていてわかりやすかったです!ありがとうございました!
数狂さん
2023-06-21 10:30:07
判別式なんかも存在しますか?
大島学習塾さん
2023-06-22 13:32:02
はむきちさん、コメントありがとうございます。
お役に立てて幸いです^^
お役に立てて幸いです^^
大島学習塾さん
2023-06-22 13:37:05
数狂さん、コメントありがとうございます。
3次以上の方程式の場合でも判別式は存在します。
「高校数学の美しい物語」さんでも記事が見つかります。
いろいろ検索してみてください^^
3次以上の方程式の場合でも判別式は存在します。
「高校数学の美しい物語」さんでも記事が見つかります。
いろいろ検索してみてください^^
新輝 佑志さん
2023-07-13 17:23:46
現在中3です。
2次方程式をやっている際に、ふと3時方程式が気になったので、参考にさせて頂きました。素人質問ですが、解に虚数解がある時もこの公式は使えますか?
とても楽しい時間でした
2次方程式をやっている際に、ふと3時方程式が気になったので、参考にさせて頂きました。素人質問ですが、解に虚数解がある時もこの公式は使えますか?
とても楽しい時間でした
大島学習塾さん
2023-07-13 22:36:50
新輝 佑志さん、コメントありがとうございます。
虚数解をもつ場合にも使えます。
ただし、係数が虚数の場合には、記事の中でとったように立方根を注意して選ぶ必要があると思います。
今後も数学の勉強を頑張ってください!
虚数解をもつ場合にも使えます。
ただし、係数が虚数の場合には、記事の中でとったように立方根を注意して選ぶ必要があると思います。
今後も数学の勉強を頑張ってください!
とととさん
2024-02-11 21:00:16
中1です。たまたま見つけたので見てみると感動しました。
本当にありがとうございます!
本当にありがとうございます!
大島学習塾さん
2024-02-14 22:28:41
ととと さん、コメントありがとうございます。
若い人が数学について感動してくれると嬉しくなります。
数学の勉強、頑張ってください!
若い人が数学について感動してくれると嬉しくなります。
数学の勉強、頑張ってください!
匿名さん
2024-05-24 11:42:18
ありがとう
lQ182のバカ(little quality)さん
2024-05-26 22:51:13
勉強なりました。小学生です!
大島学習塾さん
2024-05-27 11:15:10
匿名さん、こちらこそありがとうございます。
大島学習塾さん
2024-05-27 11:17:12
lQ182のバカ(little quality)さん、コメントありがとうございます。
若い方の勉強の役に立つのが一番嬉しいです。
若い方の勉強の役に立つのが一番嬉しいです。
あざらしさん
2024-07-11 10:44:22
わかりやすい!!
kiriさん
2024-08-22 13:04:52
すげえ二次方程式の式の形も美しさがあって好きだったけど三次方程式にもなると長すぎてもはや芸術以上のレベルに見えてきますね。僕は数学が好きなのでもっといろんな公式とか定理とか調べたりしてみたいです。ちなみに四次方程式の公式はめちゃ長いらしいですのでぜひ調べてみてください(笑)長文失礼しました。
大島学習塾さん
2024-08-23 12:38:48
あざらしさん、コメントありがとうございます。
返信が遅くなり申し訳ございません。
そう言ってもらえると励みになります!
返信が遅くなり申し訳ございません。
そう言ってもらえると励みになります!
大島学習塾さん
2024-08-23 12:47:53
kiriさん、コメントありがとうございます。
私も、数式の長短によらず、数学の公式には芸術作品に似た感動があると思います^^
4次方程式の解の公式についても記事にしております。
https://oshima-gakushujuku.com/blog/math/formula-quartic-equation/
よかったらご覧ください。
私も、数式の長短によらず、数学の公式には芸術作品に似た感動があると思います^^
4次方程式の解の公式についても記事にしております。
https://oshima-gakushujuku.com/blog/math/formula-quartic-equation/
よかったらご覧ください。
なむさん
2024-10-21 09:40:25
素晴らしい記事。
読んでいて気になったのですが、整数係数の三次方程式で、異なる3つの無理数解を持つものはあると言えますか?
読んでいて気になったのですが、整数係数の三次方程式で、異なる3つの無理数解を持つものはあると言えますか?
大島学習塾さん
2024-10-21 10:08:50
なむさん、コメントありがとうございます。
例えば、3次方程式
x^3+x^2-2x-1=0
の3つの解は、
x=2cos(2π/7), 2cos(4π/7), 2cos(6π/7)
であり、3つとも無理数となります。
他にも面白い例はたくさんあると思います。
是非、探求してみてください。
例えば、3次方程式
x^3+x^2-2x-1=0
の3つの解は、
x=2cos(2π/7), 2cos(4π/7), 2cos(6π/7)
であり、3つとも無理数となります。
他にも面白い例はたくさんあると思います。
是非、探求してみてください。
数学中毒さん
2024-11-22 08:29:49
わかりやすかったです
大島学習塾さん
2024-11-24 12:29:45
数学中毒さん、コメントありがとうございます。
「わかりやすい」と言って頂けるのが励みになります。
最近、まったく更新できていませんが、
今後とも当ブログをよろしくお願いいたします。
「わかりやすい」と言って頂けるのが励みになります。
最近、まったく更新できていませんが、
今後とも当ブログをよろしくお願いいたします。
ばらやんさん
2024-12-06 09:07:44
三次方程式の解の公式ご教授頂きありがとうございます。ガロア理論の本を買って読んでいるのですが、群論の理解が追い付いていなくてなかなか前へ進めません。群論の理解に役立つ本をご紹介頂ければ幸甚です。
大島学習塾さん
2024-12-07 14:42:21
ばらやんさん、コメントありがとうございます。
群論やガロア理論は、大学の数学科で学んだものの、その後の研究で使うこともほとんどなく(専門は解析でした^^)、学習の道を示すような知識は全くないのですが、学生時代から、
新妻 弘・木村 哲三/著『群・環・体入門』(共立出版)
横井英夫/硲野敏博 共著『代数演習』(サイエンス社)
の2冊は所有しており、ときどき参照しています。
私が大学を卒業した後に出版され、読んだことはないのですが、
雪江 明彦先生の本も評判が良いようです。
頼りない返信で申し訳ございません。
群論やガロア理論は、大学の数学科で学んだものの、その後の研究で使うこともほとんどなく(専門は解析でした^^)、学習の道を示すような知識は全くないのですが、学生時代から、
新妻 弘・木村 哲三/著『群・環・体入門』(共立出版)
横井英夫/硲野敏博 共著『代数演習』(サイエンス社)
の2冊は所有しており、ときどき参照しています。
私が大学を卒業した後に出版され、読んだことはないのですが、
雪江 明彦先生の本も評判が良いようです。
頼りない返信で申し訳ございません。
ニックネームでも可さん
2024-12-10 17:58:25
この式のおかげで4cos^3(10°)-3cos(10°)-√(3)/2=0で分からなかったcos(10°)の値が分かりました。ありがとうございます。
数学好きさん
2024-12-24 20:55:33
長すぎて覚えられな〜い!
中3さん
2025-01-29 13:59:55
勉強になった!
かいさん
2025-04-02 21:04:41
超ヤバ!
