「2023年3月」の記事一覧
1
(2 件中 1 ~ 2 件目)
2023年3月22日
当塾ホームページ内の、各種コース・時間割の内容を、令和5年度にあわせて更新いたしました。
新年度時間割へは、
令和5年4月1日(土)
から移行いたします。
よろしくお願いいたします。
新年度時間割へは、
令和5年4月1日(土)
から移行いたします。
よろしくお願いいたします。
2023年3月16日
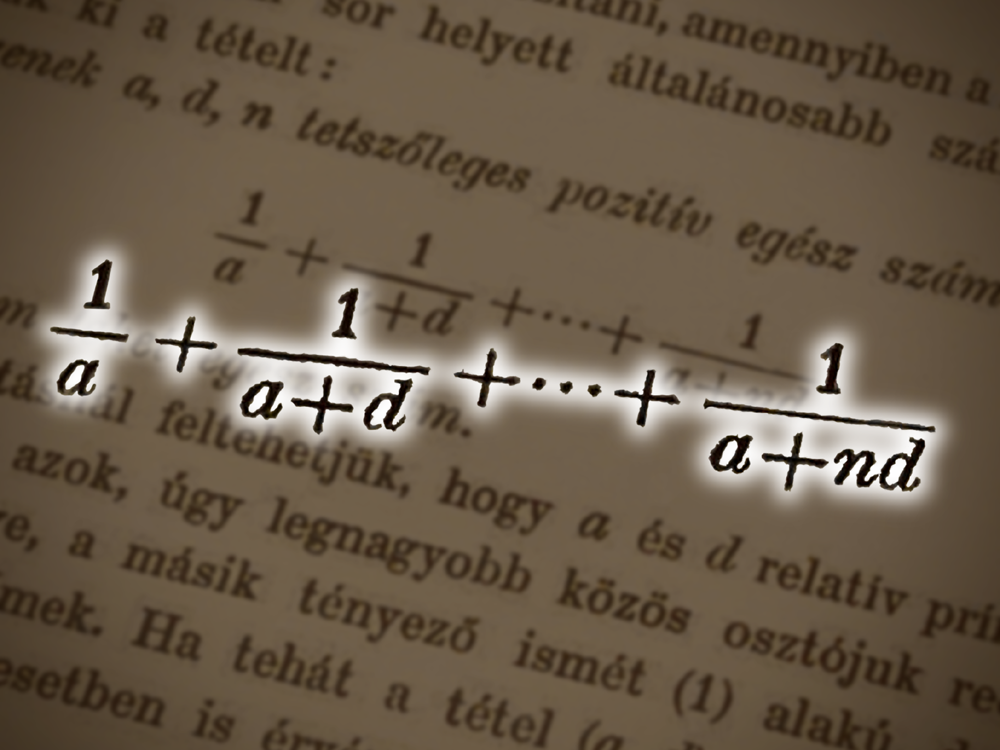
自然数 $n$ に対し,第 $n$ 調和数(harmonic number)$H_n$ を
$n\geqq 2$のとき,$H_n$の値は整数にならないことが知られています.
これは割と有名な結果で,高校生向けの受験参考書にも証明問題が掲載されているのを見たことがあります($n$ が素数の場合が出題されていたと記憶しています).
この結果にはいろいろな拡張が知られていますが,それらの一部をまとめると次のようになります:
きれいに段階的な拡張になっていますね!
この記事では,定理3の証明を最終目標に,途中で定理2の証明もご紹介します.
\[ H_n=1+\dfrac{1}{2}+\dfrac{1}{3}+\cdots+\dfrac{1}{n} \]
と定義します.$n\geqq 2$のとき,$H_n$の値は整数にならないことが知られています.
これは割と有名な結果で,高校生向けの受験参考書にも証明問題が掲載されているのを見たことがあります($n$ が素数の場合が出題されていたと記憶しています).
この結果にはいろいろな拡張が知られていますが,それらの一部をまとめると次のようになります:
定理1(タイシンガー,1915年)
$n$ を $2$ 以上の整数とするとき,
\[ 1+\dfrac12+\dfrac13+\dots+\dfrac1n \]
は整数にならない.
定理2(クルシャーク,1918年)
$a$,$n$ を正の整数とするとき,
\[ \dfrac{1}{a}+\dfrac{1}{a+1}+\dots+\dfrac{1}{a+n} \]
は整数にならない.
定理3(エルデシュ,1932年)
$a$,$d$,$n$ を正の整数とするとき,
\[ \dfrac{1}{a}+\dfrac{1}{a+d}+\cdots+\dfrac{1}{a+nd} \]
は整数にならない.
この記事では,定理3の証明を最終目標に,途中で定理2の証明もご紹介します.
1
(2 件中 1 ~ 2 件目)
