大島学習塾のブログ

解説の前に…
『数学ゴールデン』第１巻第１話に登場した、組み合わせに関する問題はコチラの記事で紹介しています： 合わせてご覧になってください！
また、『数学ゴールデン』をまだ読んでないよ～という数学好きな方はぜひ一度読んでみてください： 超オススメですッ！！

それでは、解説に移りましょう。

実験してみる

まず、式をジッと眺めてみて因数分解などができないか考えます。今回の方程式はシンプルであるがゆえに、うまい変形などあまりなさそう…。また、変数が３つあるので、１つの変数の関数とみる方法も使いにくそうです。

そこで、 $a$，$b$ に小さな値を代入して実験をしてみることにしました。このタイプの問題では、いろいろ代入してみて解の様子をみるのも常套手段の一つです！

$a$，$b$ に $1$ から $10$ までの数を代入したときの $2^a+3^b+1$ の値を，表計算ソフトを使って計算してみました： この中で値が $6^c$ と表されるものはオレンジ色に塗った３組だけです。つまり、この範囲内では解として \[ (1,1,1)，(3,3,2)，(5,1,2) \quad\cdots\,(\ast)\] の３組が見つかりました。

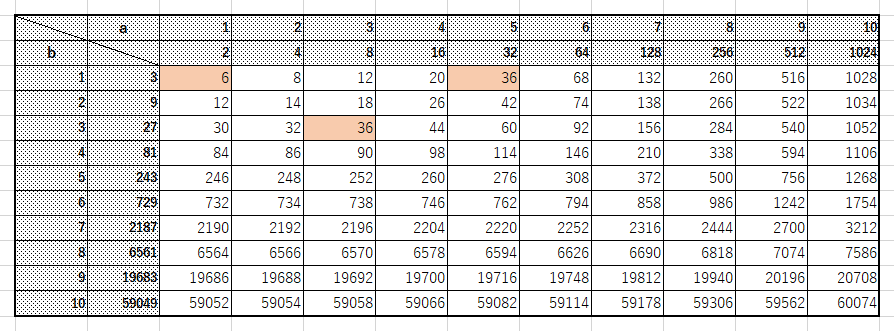
実際にはこの３組の他にももっと大きな解が存在するかもしれませんが、この問題が数学オリンピックの問題であることから、あまり大きな解は手計算では確認が難しいかなと考え、解がこの３組しか存在しないのではないかと予想しました。

６を法とする場合

方程式の解が $(\ast)$ の３組しかないことを示すため、まずは解が存在するときに $a$，$b$，$c$ がみたすべき条件をいろいろ探っていきます。
まず、方程式の右辺が $6$ の倍数になっているので、$6$ を法とする場合で考えてみましょう。
以下の計算では合同式を使います。
合同式について知らないよ～という方は参考書で調べたりネットで検索したりしてみてください。
当塾の「数学公式集」でも合同式について簡単に説明しています： $a=1$，$2$，$3$，$4$，$5$，$\cdots$ と順に代入してみると、 \[ 2^a\equiv 2，4，2，4，2，\cdots \pmod{6} \] となり、$a$ が奇数のときには $2$、偶数のときには $4$ となることが分かりました。このように、累乗数は合同式を考えると周期性をもちます。
$b=1$，$2$，$3$，$4$，$5$，$\cdots$ と順に代入してみると、 \[ 3^b\equiv 3，3，3，3，3，\cdots \pmod{6} \] となり、常に $3$ となることが分かりました。
以上の結果を合わせると、$a$ が奇数のとき、 \[ 2^a+3^b+1\equiv 2+3+1\equiv 0\pmod{6} \] $a$ が偶数のとき、 \[ 2^a+3^b+1\equiv 4+3+1\equiv 2\pmod{6} \] となり、$a$ が奇数の場合しか解が存在しないことが分かりました。
$(\ast)$ の３つの解も、$a$ はすべて奇数になっていますね！

試行錯誤の末に…

$6$ を法とする場合の議論から、方程式が解をもつには $a$ が奇数でなければならないと分かりました。一歩前進ではありますが奇数は無数にあるので、ゴールまではまだ遠いです。

今、解は $(\ast)$ の３組しかないと「予想」しています。特に $a=1$ の場合は、解は $b=1$，$c=1$ の１組のみです（…と思う）。そこで、$a=1$ のとき、どんな様子で解が１つしかないか（あるいは他にもあるか）を調べてみることにしました。
$a=1$ のとき、方程式は \[ 2^a+3^b+1=2+3^b+1=3^b+3=6^c \] となり、左辺は $3$ の倍数になります。
…とここまで計算して「あっ！」と気づきました！！左辺の式は $3$ の倍数になりますが $9$ の倍数にはなりません！対して右辺の式は $c\geqq 2$ のとき $9$ の倍数になるので両辺は一致しません。よって、解が存在する可能性があるのは $c=1$ のときのみで、この場合が $(a,b,c)=(1,1,1)$ という解に対応します。

同様の方法で「解の絞り込み」ができそうです。つまり、$2^a+1$ が $3$ でちょうど $n$ 回割り切れるとき、方程式 \[ 2^a+3^b+1=6^c \] において、$b\lt n$ ならば、左辺は $3$ でちょうど $b$ 回しか割り切れず、$n\leqq b$ ならば、左辺は $3$ でちょうど $n$ 回しか割り切れないので、いずれの場合も $c\leqq n$ となることが分かります。

この「絞り込み」の様子を次の奇数 $a=3$ の場合で確かめてみました。
$a=3$ のとき、方程式は \[ 2^a+3^b+1=8+3^b+1=3^b+9=6^c \] となって左辺は $3$ で最大$2$ 回しか割り切れないので、$c\leqq 2$ となります。$c=1$，$2$ を順に試すと、この場合の解は $(a,b,c)=(3,3,2)$ しか存在しないことが分かります。
このように、$a=3$ の場合は「解の絞り込み」がうまくいったのですが、なんとなく一般の場合の証明はうまくいかなそうな雰囲気です。$a=9$ の場合は、 \[ 2^9+1=513=3^3\times 19 \] なので、「絞り込み」の範囲を $c\leqq 3$ に広げる必要があります。同様に $a$ の選び方によっては $2^a+1$ が $3$ で割り切れる回数はいくらでも大きくできて、「絞り込み」の範囲を有限にはできないように見えます。

このままではうまくいきそうにありませんが、この方法に可能性を感じたので、状況の整理も含めて、同様のアイディアを $2$ の累乗の方でも試してみることにしました。
まずは、手始めに $2^2=4$ を法とした場合を考えてみました。
$b=1$，$2$，$3$，$4$，$5$，$\cdots$ と順に代入してみると、 \[ 3^b\equiv 3，1，3，1，3，\cdots \pmod{4} \] なので、$b$ が奇数のとき、 \[ 2^a+3^b+1\equiv 2^a+4\equiv 2^a \pmod{4} \] $b$ が偶数のとき、 \[ 2^a+3^b+1\equiv 2^a+2\pmod{4} \] となり、$b$ が奇数のときには解を絞り込めません！

次は $2^3=8$ を法とした場合です。
$b=1$，$2$，$3$，$4$，$5$，$\cdots$ と順に代入してみると、 \[ 3^b\equiv 3，1，3，1，3，\cdots \pmod{8} \] なので、$b$ が奇数のとき、 \[ 2^a+3^b+1\equiv 2^a+4 \pmod{8} \] $b$ が偶数のとき、 \[ 2^a+3^b+1\equiv 2^a+2 \pmod{8} \] となり、$a\geqq 3$ のとき $2^a+3^b+1$ は $8$ の倍数にならないことが分かりました。$c\geqq 3$ のとき $6^c$ は $8$ の倍数になるので、これは解の絞り込みに成功しています！！

解答

これまでに得たアイディアを解答にまとめましょう！

おわりに

今回は、私が初めて問題を解いたときの計算用紙をもとに記事を書いてみました^^♪
初めから方針が定まっているワケではなく、いろいろ試行錯誤しながら解法の糸口をつかんでいる様が見て取れたのではないかと思います。
「難問」に取り組むときの姿勢など、参考になる部分があれば幸いです。

2021年度の日本数学オリンピックの予選が１月11日に行われました（今年はオンラインで実施されました）。『数学ゴールデン』がきっかけで受験した方も、もしかしたらいるかもしれません。彼らの中から成績優秀な者が選抜され、日本代表が選ばれていきます。そしてそれは『数学ゴールデン』の主人公たちも歩む道です。そう考えると胸が熱くなりますね！！^^

『数学ゴールデン第２巻』は２月26日発売予定だそうです。２巻ではどんなドラマが展開され、どんな難問が主人公たちに立ちふさがるのでしょうか！？すごく楽しみです！！